GRE Arithmetic And Algebra

Quant preparation will be covered in this course and this is the first article that will cover both Arithmetic and Algebra Part. So let's start...

GRE Quant  Arithmetic

The GRE Quant section tests how well you can think critically and solve problems using basic math concepts. It might seem tough at first, but really, it's mostly about math you’ve already learned in school. It’s not about advanced math, but more about understanding numbers, ratios, percentages, and how to use them in real-life situations.

Key Arithmetic Topics You’ll Encounter:

1. Number Theory
2. Ratios
3. Percentages
4. Application-Based Problems

These topics make up a significant portion of the questions you’ll face in the GRE Quantitative section, so mastering them is essential for scoring well.

Number Theory

Number theory is often referred to as the "queen of mathematics." It is a branch of math that deals with the properties of numbers, including prime numbers, divisibility, and factors. For GRE purposes, you’ll need to understand a few key concepts within this area.

Key Concepts in Number Theory:

• Properties of Integers: This includes understanding different types of numbers, such as prime numbers, even and odd numbers, and whole numbers. You'll also need to know about divisibility rules, greatest common factors (GCF), least common multiples (LCM), and the concept of remainders.
• Fractions: You’ll need to be familiar with fractions, including operations on fractions, comparisons, and converting them to decimals and percentages. Be sure to practice solving problems where you must manipulate fractions and decimals. It’s also key to know how to convert fractions to decimals and percentages, like turning 1/21​ into 0.5 or 50%. Many problems will require you to switch between fractions and decimals, so practice those conversions.
• Exponents and Roots: GRE number theory questions may test your ability to handle exponents, scientific notation, and square or cube roots. You'll need to understand the laws of exponents, such as when multiplying or dividing numbers with the same base, and how to simplify roots.                                                                                                                           

Sample Number Theory Question:

1.  What is the greatest common divisor (GCD) of 252 and 315?
Solution:

2. What is the least common multiple (LCM) of 18 and 24?
Solution:

3. How many divisors does 180 have?
Solution:

4. What is the remainder when 925 is divided by 17?
Solution:
Dividing 925 by 17 gives a quotient of 54 and a remainder of 7.
So, the remainder is 7.

5. How many even prime numbers are there?
Solution:
There is only one even prime number, which is 2.

6. If twice 4,632 is divided by 100, what is the tenths digit?
Answer:
4,632 × 2 = 9,264.
9,264 ÷ 100 = 92.64.
The tenth digit is 6.

7. If 617 is divided by 49, the sum of the tens digit and the tenths digit is equal to…
Answer:
617 ÷ 49 ≈ 12.6122.
The tens digit is 1, and the tenth digit is 6.
The sum is 7.

8. Quantity A: The age at death, in years and days, of a person who lived from January 31, 1817 to January 15, 1901.
Quantity B: The age at death, in years and days, of a person who lived from January 15, 1904 to January 31, 1988.
Answer:

• For Quantity A: From January 31, 1817, to January 15, 1901, the person lived for 83 years, 11 months, and 15 days.
• For Quantity B: From January 15, 1904, to January 31, 1988, the person lived for 84 years, 16 days.

The age at death for Quantity B is greater by 1 year and 16 days.

9. 25 employees donated a total of $450 to charity. If 15 employees donated at least $12 and 9 employees donated at least $19, what is the maximum amount, in dollars, that the last employee could have donated?
Answer:
Total donation = $450.
Donation from 15 employees = 15 × $12 = $180.
Donation from 9 employees = 9 × $19 = $171.
Remaining amount = $450 − ($180 + $171) = $99.
Therefore, the last employee could have donated $99.

10. Out of 5.5 billion bacteria grown for an experiment, 1 in 75 million has a particular mutation. Approximately how many of the bacteria have the mutation?
Answer:
Total bacteria = 5.5 billion.
Number with mutation = (5.5 billion ÷ 75 million) = 73.

11. A particular nation’s GDP (Gross Domestic Product) is $4.5 billion. If the population of the nation is 1.75 million, what is the per capita (per person) GDP, rounded to the nearest dollar?
Answer:
Per capita GDP = $4.5 billion ÷ 1.75 million = $2,571.

12. Global GDP (Gross Domestic Product) was $69.97 trillion in 2011. If the world population for 2011 was best estimated at 6,973,738,433, approximately what is the global GDP per person?
Answer:
Global GDP per person = $69.97 trillion ÷ 6,973,738,433 = $10,000.

Ratios

Ratios are a vital concept on the GRE, as they appear in both direct problems and applied word problems. You’ll need to understand the relationship between two or more numbers expressed as a ratio and how to manipulate these ratios in various situations.

Key Concepts in Ratios:

• Understanding Ratios: A ratio expresses the relationship between two quantities. For example, the ratio of boys to girls in a classroom might be written as 2:3.
• Proportions: A proportion is an equation stating that two ratios are equal. GRE problems may ask you to solve for an unknown using proportional relationships.
• Word Problems Involving Ratios: Often, you’ll face complex word problems where you need to apply your knowledge of ratios. For example, the ratio of workers to output, or the ratio of ingredients in a recipe.

Sample Ratio Question:
1. In a class of 30 students, the ratio of boys to girls is 4:5. How many girls are in the class?

Solution:

2. In a box of red and blue marbles, the ratio of red marbles to blue marbles is 5:7. If there are 84 blue marbles, how many red marbles are there?
Solution:

3. Children and adults in the group based on ticket cost.
A group of 20 people went to a concert. The cost of an adult ticket was $12, and the cost of a children’s ticket was $8. The total cost of tickets for the group was $192. How many adults and how many children were in the group?

Answer:
Let the number of adults be x and the number of children be y.
We know the total number of people is 20, so:
x + y = 20.

Also, the total cost of tickets is $192, so:
12x + 8y = 192.

Solving this system of equations:
From x + y = 20, we can substitute y = 20 - x into the second equation:
12x + 8(20 - x) = 192.
Simplifying:
12x + 160 - 8x = 192,
4x = 32,
x = 8.

So, there are 12 adults and 8 children in the group.

4. Mitchell’s total pay during the 8-week camp.
Mitchell worked at a summer camp for 8 weeks, and he was paid $125 per week. How much did he earn in total for the 8 weeks?

Answer:
Mitchell’s total pay is calculated by multiplying his weekly pay by the number of weeks:
$125 × 8 = $1,000.
So, Mitchell’s total pay during the 8-week camp is $1,000.

5. Price per word for the book vs. short story.
A writer is paid for both a book and a short story. The book is priced at $4,500 for 60,000 words, and the short story is priced at $900 for 12,000 words. What is the price per word for both the book and the short story? How do they compare?

Answer:
For the book:
Price per word = 4,500 ÷ 60,000 = $0.075 per word.

For the short story:
Price per word = 900 ÷ 12,000 = $0.075 per word.

Both the book and the short story have the same price per word of $0.075.

6. How many gallons needed to fill the tank to 3/10 of its capacity.
A gas tank holds 80 gallons. How many gallons are needed to fill the tank to 3/10 of its capacity?

Answer:
To fill the tank to 3/10 of its capacity, we multiply the total capacity by 3/10:
80 × (3/10) = 24 gallons.
So, 24 gallons are needed to fill the tank to 3/10 of its capacity.

7. Kilograms to pounds conversion and comparison.
Convert the following weights from kilograms to pounds, and then compare them:

• 20 kilograms
• 60 kilograms

(Use the conversion factor: 1 kilogram = 2.2 pounds.)

Answer:
For 20 kilograms:
20 × 2.2 = 44 pounds.

For 60 kilograms:
60 × 2.2 = 132 pounds.

Comparing the two values, 132 pounds is greater than 44 pounds.

8. Number of seconds in 12 hours vs. the number of minutes in 720 hours.
How many seconds are there in 12 hours?
How many minutes are there in 720 hours?

Answer:
To find the number of seconds in 12 hours:
12 × 60 × 60 = 43,200 seconds.

To find the number of minutes in 720 hours:
720 × 60 = 43,200 minutes.

So, the number of seconds in 12 hours (43,200) is equal to the number of minutes in 720 hours (43,200).

9. Joe’s car travel distance in kilometers based on fuel.
Joe’s car uses 6 liters of fuel for every 100 kilometers traveled. If Joe has 18 liters of fuel, how far can he travel in kilometers?

Answer:
To find the distance Joe can travel, we use the ratio of liters to kilometers:
(18 ÷ 6) × 100 = 300 kilometers.
So, Joe can travel 300 kilometers with 18 liters of fuel.

Percentages

Percentages are another major player in the GRE Quant section. Understanding how to work with percentages, calculate percentage increases and decreases, and solve percentage-based word problems will give you a huge advantage.

Key Concepts in Percentages:

• Basic Percentage Calculations: These involve calculating a certain percentage of a number or determining what percentage one number is of another. For example, what is 25% of 60? You might also need to figure out what percentage one number is of another.
• Percentage Increase/Decrease: You will need to calculate how much a number increases or decreases by a certain percentage. 
  • For example, if something costs $50 and goes up by 20%, you add 20% of $50 (which is $10) to get the new price of $60. Understanding this concept is crucial for problems that talk about price changes, salary hikes, or population growth.
• Successive Percentage Change: When percentage changes happen one after another, you need to use a formula to calculate the final result.

Sample Percentage Question:
1. The price of a jacket was $80, and it increased by 10%. What is the new price?

Solution:
To calculate the new price, multiply the original price by the percentage increase:

8880×1.10=88

The new price is $88.

2. A population increases by 15% in the first year and by 10% in the second year. If the initial population is 800, what is the population after two years?
Solution:
After the first year: 800×1.15=920
After the second year: 920×1.10=1012
The population after two years is 1012.

3. The price of a product decreased by 20% and is now $120. What was the original price?
Solution: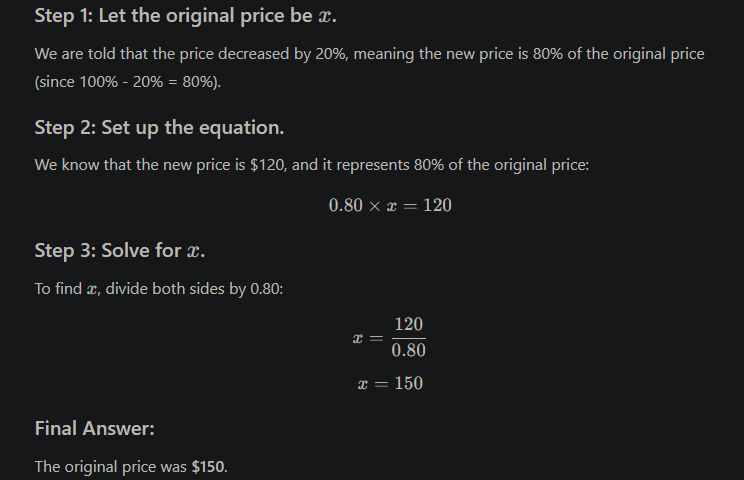

4. A test has 60 questions. If you answer 48 questions correctly, what is your score as a percentage?
Solution:
The percentage score is 48/60×100=80%

5. A company had a profit of $500,000 last year. This year, the profit increased by 25%. What is this year's profit?
Solution:
This year’s profit is 500,000×1.25=625,000

6. A student scored 80% on a test, which had 50 questions. How many questions did the student answer correctly?
Solution:
The number of correct answers is 0.80×50=40

7. Comparing coffee costs at Ali’s and Bob’s coffee shops.
Ali’s Coffee Shop sells a cup of coffee for $4, and Bob’s Coffee Shop sells a cup for $4.50. What percentage more expensive is Bob’s coffee compared to Ali’s coffee?

Answer:
To find the percentage difference:
Price difference = $4.50 - $4 = $0.50.

To find the percentage increase relative to Ali’s price:
($0.50 ÷ $4) × 100 = 12.5%.

So, Bob’s coffee is 12.5% more expensive than Ali’s coffee.

8. Taxi driver’s profit considering hourly wage, rent, and costs.
A taxi driver earns $15 per hour and works for 8 hours. His rent for the taxi is $100 per day, and he spends $30 on fuel each day. What is his profit after working for the day?

Answer:
The total earnings from working 8 hours is:
$15 × 8 = $120.

The total expenses are:
Rent + Fuel = $100 + $30 = $130.

To find the profit:
Earnings - Expenses = $120 - $130 = -$10.

So, the taxi driver has a $10 loss after working for the day.

9. Per-tissue cost comparison for Softies and Enviro tissues.
A box of Softies tissues costs $6.00 for 200 tissues, and a box of Enviro tissues costs $7.50 for 250 tissues. Which box has a lower per-tissue cost, and by what percentage?

Answer:
For Softies tissues:
Cost per tissue = $6.00 ÷ 200 = $0.03 per tissue.

For Enviro tissues:
Cost per tissue = $7.50 ÷ 250 = $0.03 per tissue.

Both Softies and Enviro tissues have the same cost of $0.03 per tissue, so there is no difference in per-tissue cost.

Application-Based Problems

This category of arithmetic tests your ability to apply basic concepts like number theory, ratios, and percentages to real-life scenarios. These questions often involve word problems and require a strong understanding of the application of mathematical concepts in different contexts.

Key Application-Based Topics:

• Profit and Loss: These problems often involve percentages, where you calculate profit or loss as a percentage of cost price (CP) or selling price (SP).

For example, if you buy something for $100 and sell it for $120, you have a profit of $20, which is 20% profit based on the cost price.

• Interest Calculations: These problems may ask about simple interest or compound interest, requiring you to understand percentage change and apply formulas for interest.

Interest = Principal × Rate × Time

• Time and Work, Time and Distance: These concepts, often applied in ratio problems, test your understanding of rates and speed or work rates.

These problems often rely on ratios, like "If someone works at a rate of 5 tasks per hour, how long will it take to finish 20 tasks?"

Sample Application Problem:

1. A shopkeeper bought a shirt for $50 and sold it for $60. What is his percentage profit?

Solution:
Here, the profit is $60 - $50 = $10. So:

Profit Percentage=(10/50)×100=20%

The profit percentage is 20%.

2. A store sells a laptop for $800 after applying a 10% discount. What was the original price of the laptop?
Solution:

3. A car travels 45 miles per hour. How long will it take to travel 180 miles?
Solution:
The time required is 180/45=4 hours

4. An investment of $1000 is made at a rate of 8% per annum, compounded annually. What is the value of the investment after 3 years?
Solution:

5. A worker is paid $12 per hour for the first 40 hours worked. For overtime, they are paid 1.5 times the regular hourly rate. How much will the worker earn if they work 50 hours in a week?
Solution:
For the first 40 hours: 40×12=480
For the 10 overtime hours: 10×(12×1.5)=10×18=180
Total earnings = 480+180=660480 + 180 = 660480+180=660.
The worker will earn $660.

6. A factory produces 240 units per day. How many units will it produce in 45 days?
Solution:
The total number of units produced in 45 days is 240×45=10,800 units

7. Formula conversion from Fahrenheit to Celsius.
Convert 98.6°F to Celsius using the formula:
C = (F - 32) × 5/9.

Answer:
Substitute 98.6°F into the formula:
C = (98.6 - 32) × 5/9
C = (66.6) × 5/9
C = 333/9
C ≈ 37°C.

So, 98.6°F is approximately 37°C.

8. Conversion of feet based on changes in foot length (historical).
If 1 foot was historically defined as 12 inches, and then was redefined to 30.48 centimeters, how many feet are in 100 inches?

Answer:
First, convert 100 inches to feet using the historical definition:
100 ÷ 12 = 8.33 feet (approximately).

Now, convert 100 inches to feet based on the redefined definition (1 foot = 30.48 cm).
First, convert 100 inches to centimeters:
100 inches × 2.54 cm/inch = 254 cm.

Now, convert 254 cm to feet:
254 ÷ 30.48 ≈ 8.33 feet.

So, based on both definitions, 100 inches equals approximately 8.33 feet.

9. Number of tapes problem (Mary, Pedro, and John’s tape sharing).
Mary has 15 meters of tape. Pedro has 20 meters, and John has 25 meters. If they decide to share the tape equally, how much tape will each person get?

Answer:
Total tape = 15 + 20 + 25 = 60 meters.

Dividing the tape equally among the three people:
60 ÷ 3 = 20 meters.

So, each person will get 20 meters of tape.

10. Dividing candies among cousins.
Emma has 48 candies. She wants to divide them equally among 6 cousins. How many candies will each cousin receive?

Answer:
Total candies = 48.
Number of cousins = 6.

Divide the candies equally:
48 ÷ 6 = 8.

So, each cousin will receive 8 candies.

Mixed Arithmetic

1. Quantitative comparison (expression comparison with nested parentheses).
Which is greater: (5 + 3) × (8 - 4) or 6 × (7 + 2)?

Answer:
For (5 + 3) × (8 - 4):
First, simplify inside the parentheses:
(5 + 3) = 8 and (8 - 4) = 4.
Now, calculate:
8 × 4 = 32.

For 6 × (7 + 2):
Simplify inside the parentheses:
(7 + 2) = 9, then calculate:
6 × 9 = 54.

Since 32 is less than 54, the second expression is greater.

2. Quantitative comparison (multiplication and addition expressions).
Which is greater: 4 × (6 + 5) or 5 × (7 + 3)?

Answer:
For 4 × (6 + 5):
Simplify inside the parentheses:
(6 + 5) = 11, then calculate:
4 × 11 = 44.

For 5 × (7 + 3):
Simplify inside the parentheses:
(7 + 3) = 10, then calculate:
5 × 10 = 50.

Since 44 is less than 50, the second expression is greater.

3. Quantitative comparison involving powers of numbers.
Which is greater: 3² × 4³ or 5³ × 2³?

Answer:
For 3² × 4³:
3² = 9 and 4³ = 64, so:
9 × 64 = 576.

For 5³ × 2³:
5³ = 125 and 2³ = 8, so:
125 × 8 = 1000.

Since 576 is less than 1000, the second expression is greater.

4. Quantitative comparison with square terms and subtraction.
Which is greater: (8² - 3²) or (6² + 2²)?

Answer:
For (8² - 3²):
8² = 64 and 3² = 9, so:
64 - 9 = 55.

For (6² + 2²):
6² = 36 and 2² = 4, so:
36 + 4 = 40.

Since 55 is greater than 40, the first expression is greater.

5. Multiplication of large numbers.
What is the product of 928 × 625?

Answer:
928 × 625 = 580,000.

So, the product is 580,000.

6. Admission cost comparison for a family visiting the museum.
A family of 4 adults and 3 children visits a museum. The adult ticket costs $12 and the child ticket costs $8. What is the total admission cost?

Answer:
The cost for 4 adults:
4 × 12 = $48.

The cost for 3 children:
3 × 8 = $24.

Total admission cost:
48 + 24 = $72.

So, the total admission cost is $72.

7. Pool losing water (conversion from milliliters to liters per hour).
A pool is losing water at a rate of 1500 milliliters per hour. Convert this to liters per hour.

Answer:
Since 1 liter = 1000 milliliters, convert 1500 milliliters to liters:
1500 ÷ 1000 = 1.5 liters.

So, the pool is losing 1.5 liters of water per hour.

8. Chocolate consumption problem (Child A vs. Child B).
Child A eats 4 pieces of chocolate every day, while Child B eats 5 pieces per day. How many pieces will each child eat after 7 days?

Answer:
For Child A:
4 pieces × 7 days = 28 pieces.

For Child B:
5 pieces × 7 days = 35 pieces.

So, after 7 days, Child A will eat 28 pieces and Child B will eat 35 pieces.

9. Cost of wood for making frames, based on wood pricing.
A frame requires 3 meters of wood. The cost of the wood is $10 per meter. How much will it cost to make 5 frames?

Answer:
The wood required for 5 frames:
3 meters × 5 frames = 15 meters.

The total cost:
15 meters × $10 = $150.

So, the total cost to make 5 frames is $150.

10. Time taken to travel from Earth to Mercury based on distance and speed.
The distance from Earth to Mercury is approximately 92 million kilometers. If a spacecraft travels at a speed of 30,000 kilometers per hour, how long will it take to reach Mercury?

Answer:
Time = Distance ÷ Speed
Time = 92,000,000 ÷ 30,000 = 3066.67 hours.

To convert hours into days:
3066.67 ÷ 24 ≈ 127.78 days.

So, it will take approximately 127.78 days to travel from Earth to Mercury.

GRE Quant Algebra 

Algebra is a key part of the GRE Quantitative section, and it’s all about solving problems that involve variables (like xxx, yyy, etc.), numbers, and different mathematical operations. Don’t worry if you find algebra a little tricky at first—once you understand the basics and practice, you’ll be able to solve most problems with confidence. This guide will walk you through different algebra topics you’ll face in the GRE Quantitative section, using clear and simple explanations, with plenty of examples.

Simplifying Algebraic Expressions

When you're asked to simplify algebraic expressions, your goal is to combine like terms and make the expression as simple as possible. Think of it like cleaning up a messy room—organizing things into groups and making everything neat.

What are like terms?
Terms are terms that have the same variable and the same power. For example, 3x3x3x and 5x5x5x are like terms because both have the variable xxx. You can combine them by adding or subtracting their coefficients (the numbers in front).

Steps to Simplify:

• Combine like terms (terms with the same variable and exponent).
• Use the distributive property when needed (multiplying numbers over terms inside parentheses).

Example 1:

Simplify:
2x2+5x−3+4x2−x+72x^2 + 5x - 3 + 4x^2 - x + 72x2+5x−3+4x2−x+7.

Solution:

Example 2:

Simplify:
3(2x+4)−4(x−2)+53(2x + 4) - 4(x - 2) + 53(2x+4)−4(x−2)+5.

Solution:

• Use the distributive property:
  3(2x+4)=6x+123(2x + 4) = 6x + 123(2x+4)=6x+12,
  −4(x−2)=−4x+8-4(x - 2) = -4x + 8−4(x−2)=−4x+8.
• Combine:
  6x+12−4x+8+56x + 12 - 4x + 8 + 56x+12−4x+8+5.
• Simplify:
  (6x−4x)+(12+8+5)=2x+25(6x - 4x) + (12 + 8 + 5) = 2x + 25(6x−4x)+(12+8+5)=2x+25.

Example 3:

Simplify:
(2x + 3)/5 - {x - 4}/3

Solution:

Example 4:

Simplify:
4(x−2)+3(x+5)−2x4(x - 2) + 3(x + 5) - 2x4(x−2)+3(x+5)−2x.

Solution:

• Distribute:
  4(x−2)=4x−84(x - 2) = 4x - 84(x−2)=4x−8,
  3(x+5)=3x+153(x + 5) = 3x + 153(x+5)=3x+15.
• Combine:
  4x−8+3x+15−2x4x - 8 + 3x + 15 - 2x4x−8+3x+15−2x.
• Simplify:
  (4x+3x−2x)+(−8+15)=5x+7(4x + 3x - 2x) + (-8 + 15) = 5x + 7(4x+3x−2x)+(−8+15)=5x+7.

Solving Quadratic Equations

Quadratic equations are equations where the highest power of the variable is 2. They are in the form ax^2+bx+c=0 and can be solved using various methods like factoring, using the quadratic formula, or completing the square.

What is the quadratic formula?

The quadratic formula is used when factoring isn’t easy. It’s a formula you can apply directly to any quadratic equation to find the values of x that satisfy it. The formula is:

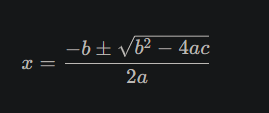
where a, b, and c are the coefficients in the quadratic equation ax2+bx+c=0ax^2 + bx + c = 0ax2+bx+c=0.

Example 1:

Solve:
x2−5x+6=0x^2 - 5x + 6 = 0x2−5x+6=0.

Solution:

• Factor the equation:
  (x−2)(x−3)=0(x - 2)(x - 3) = 0(x−2)(x−3)=0.
• So, x=2x = 2x=2 or x=3x = 3x=3.

Example 2:

Solve:
2x2−7x+3=02x^2 - 7x + 3 = 02x2−7x+3=0.

Solution:

• Use the quadratic formula:

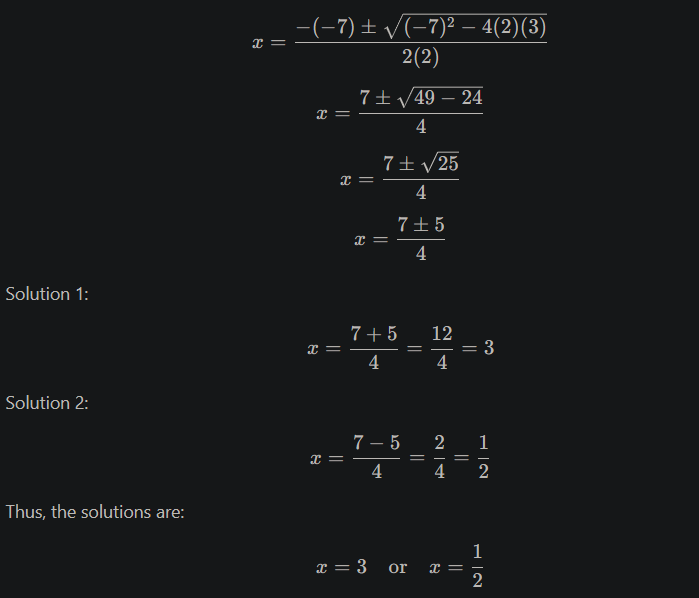
Example 3:

Solve:
x2−8x+15=0x^2 - 8x + 15 = 0x2−8x+15=0.

Solution:

• Factor the quadratic equation:
  (x−3)(x−5)=0(x - 3)(x - 5) = 0(x−3)(x−5)=0.
• So, x=3x = 3x=3 or x=5x = 5x=5.

Example 4:

Solve:
3x2+4x−5=03x^2 + 4x - 5 = 03x2+4x−5=0.

Solution:

• Use the quadratic formula:

Solving Systems of Equations

A system of equations is a set of two or more equations that have common variables. You need to find values of the variables that satisfy all equations in the system at the same time.

There are three common methods to solve a system of equations:

1. Substitution: Solve one equation for one variable, then substitute that expression into the other equation.
2. Elimination: Add or subtract equations to eliminate one of the variables.
3. Graphing: Plot both equations on a graph and find the point where they intersect.

Example 1:

Solve the system:

x+y=6x + y = 6 x+y=6 2x−y=32x - y = 32x−y=3

Solution:

• From the first equation, y=6−xy = 6 - xy=6−x.
• Substitute y=6−xy = 6 - xy=6−x into the second equation:

2x−(6−x)=32x - (6 - x) = 32x−(6−x)=3

• Simplify:

2x−6+x=3⇒3x=9⇒x=32x - 6 + x = 3

• Substitute x=3x = 3x=3 into y=6−xy = 6 - xy=6−x:

y=6−3=3y = 6 - 3 = 3y=6−3=3

Thus, x=3x = 3x=3, y=3y = 3y=3.

Example 2:

Solve the system:

3x+2y=123x + 2y = 12 3x+2y=12 4x−y=94x - y = 94x−y=9

Solution:

• From the second equation, solve for y:
  y=4x−9y = 4x - 9y=4x−9.
• Substitute into the first equation:

3x+2(4x−9)=123x + 2(4x - 9) = 123x+2(4x−9)=12

• Simplify:

Solving Exponent and Radical Equations

In algebra, exponents (powers) and radicals (roots) are often used to solve problems. An exponent shows how many times to multiply the base number by itself, and a radical is the opposite operation (finding a root).

What is an exponent?

An exponent is a small number placed above the base number. For example, 23=2×2×2=82^3 = 2 \times 2 \times 2 = 823=2×2×2=8.

What is a radical?

A radical is the opposite of an exponent. For example, the square root of 9 is 9=3\sqrt{9} = 39​=3, because 32=93^2 = 932=9.

Example 1:

Solve:
(2x)3=54(2x)^3 = 54(2x)3=54.

Solution:

Example 2:

Solve:
x+3=7\sqrt{x + 3} = 7x+3​=7.

Solution:
 

Example 3:

Solve:
2x+1=162^{x+1} = 162x+1=16.

Solution:
Express 16 as a power of 2:

16=2416 = 2^416=24

Now set the exponents equal to each other:

x+1=4⇒x=3x + 1 = 4⇒ x = 3x+1=4⇒x=3

Example 4:

Solve:
3x−1=4\sqrt{3x - 1} = 43x−1​=4.

Solution:
Square both sides:

3x−1=16⇒3x=17⇒3x - 1 = 16  ⇒3x = 17  ⇒x = {17}{3}3x−1=16⇒3x=17⇒x=317​

Mixed Algebra

1.If 3x + 2(x + 2) = 2x + 16, then x = ?

Step-by-step solution:

2.If (x + 3)² = 225, which of the following could be the value of x - 1? (A) 13
(B) 12
(C) -12
(D) -16
(E) -19

3. If x=2x = 2x=2, Quantity A and Quantity B:

We are given that:

x2−4x+3x^2 - 4x + 3x2−4x+3

Substituting x=2x = 2x=2:

(2)2−4(2)+3=4−8+3=−1(2)^2 - 4(2) + 3 = 4 - 8 + 3 = -1(2)2−4(2)+3=4−8+3=−1

The value of Quantity A is −1-1−1, so the value of Quantity B is 1.

Thus, the answer is Quantity A < Quantity B.

4. 1200x+6000=132001200x + 6000 = 132001200x+6000=13200, and 12y+60=13212y + 60 = 13212y+60=132:

First, solve for x:

Thus, the answer is Quantity A = Quantity B, so the answer is (A) x = y.

5. If 4x+3y=244x + 3y = 244x+3y=24 and 2x−y=42x - y = 42x−y=4, what is the value of x+yx + yx+y?

First, solve one of the equations for one variable. From 2x−y=42x - y = 42x−y=4, solve for y: