Introduction
Let’s face it—preparing for the GRE Quant section can feel like wrestling with math problems in a never-ending maze. But don’t worry, we’ve got your back! Some of the trickiest topics—like divisibility, prime numbers, exponents, and roots—might sound intimidating, but once you crack their secrets, they’re actually pretty manageable.
So why are these topics so important? Well, divisibility helps you figure out which numbers play nice together without all that leftover drama (hello, remainders). Prime numbers are like the VIPs of math—unique, powerful, and popping up everywhere in GRE questions. Exponents? They’re just math’s way of saying, “Let’s take it up a notch!” And roots? They help you simplify scary-looking numbers into something friendlier.
In this blog, we’ll take a fun and practical approach to mastering these GRE essentials. You’ll get simple explanations, handy tricks, and real-world examples to help you tackle these problems like a pro. By the end, you’ll not only understand these topics but actually enjoy solving them (or at least not hate them). Ready to dive in? Let’s do this!
"Mathematics is not about numbers, equations, or algorithms: it’s about understanding. Once you get the hang of it, even the toughest problems become puzzles waiting to be solved." – Anonymous
Divisibility
Short Note
The Law of Divisibility says that a number is divisible by another if, after dividing, there is no remainder. This magical rule helps you quickly check if a number is a perfect fit for another, just like finding the right puzzle piece.
- Divisibility by 2: The number must be even (last digit is 0, 2, 4, 6, or 8).
- Divisibility by 3: The sum of the digits must be divisible by 3.
- Divisibility by 5: The number must end in 0 or 5.
- Divisibility by 6: The number must be divisible by both 2 and 3.
Tips
- “Two’s company, three’s a crowd!” - If a number ends in 0 or 2, it’s a party with 2! For 3, just add up the digits—if the sum’s a friend of 3, you’ve got yourself a winner.
- Pro tip: For divisibility by 9, add the digits—if they scream “9!” (i.e., sum is divisible by 9), you’re in!
- Trick: Use divisibility rules to quickly eliminate choices. You’ll be like a math ninja cutting through options!
Example with Step by Step Solution
Question:
Which of the following numbers is divisible by both 3 and 4?
A) 126
B) 144
C) 156
D) 162
Solution:
To be divisible by both 3 and 4, the number must satisfy:
- Divisibility by 3 → Sum of digits must be divisible by 3.
- Divisibility by 4 → Last two digits of the number must be divisible by 4.
Checking each option:
126
- Sum of digits = 1 + 2 + 6 = 9 (divisible by 3 ✅)
- Last two digits = 26 (not divisible by 4 ❌)
144
- Sum of digits = 1 + 4 + 4 = 9 (divisible by 3 ✅)
- Last two digits = 44 (divisible by 4 ✅)
- ✅ Correct Answer
156
- Sum of digits = 1 + 5 + 6 = 12 (divisible by 3 ✅)
- Last two digits = 56 (divisible by 4 ✅)
- ✅ Also correct
162
- Sum of digits = 1 + 6 + 2 = 9 (divisible by 3 ✅)
- Last two digits = 62 (not divisible by 4 ❌)
Thus, the correct answers are B) 144 and C) 156.
Prime Numbers
Short Note
Prime numbers are like the elite members of the number club—they can’t be divided by anyone except 1 and themselves. Any number that has more than two factors gets kicked out.
A prime number greater than 1 is only divisible by 1 and itself. For example, 2, 3, 5, 7, 11, 13 are all prime numbers. (You get the idea!)
Tips (Prime Time!)
- Prime numbers are like introverts at a party— they don't mingle with anyone but themselves!
- Prime number tip: To find primes, check for divisibility by numbers less than the square root of the number. This speeds up the process and makes you feel like a math detective!
- “Prime time is anytime!” - Don’t get bogged down—primes come in all sizes, and the more you practice, the easier they are to spot!
Example with Step by Step Solution
Question:
Which of the following numbers is a prime number?
A) 27
B) 29
C) 35
D) 51
Solution:
A prime number is a number greater than 1 that has only two factors: 1 and itself.
Checking each option:
- 27 → Divisible by 3 and 9 (Not Prime ❌)
- 29 → Only divisible by 1 and 29 (Prime ✅)
- 35 → Divisible by 5 and 7 (Not Prime ❌)
- 51 → Divisible by 3 and 17 (Not Prime ❌)
Thus, the correct answer is B) 29.
Exponents
Short Note

Example with Step by Step Solution

Roots
Short Note

Example with Step by Step Solution

Mixed Question (Combining Exponents and Roots)

Some GRE Problems with Step by Step Solutions
Question 1
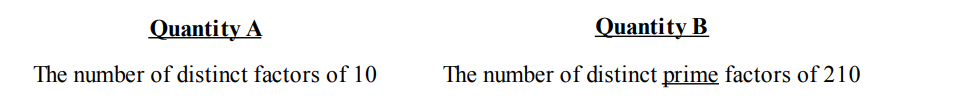
Solution:

Question 2

Solution:

Question 3

Solution:

Question 4

Solution:

Question 5

Solution:

Question 6

Solution:

Question 7

Solution:
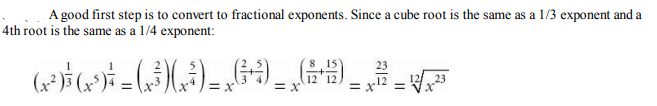
Question 8

Solution:

Question 9
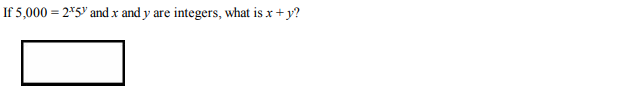
Solution:

Question 10

Solution:

Conclusion
And that’s a wrap! Divisibility, prime numbers, exponents, and roots might look like a handful of tough problems at first, but once you get the hang of them, they’re really just the building blocks of GRE success. Mastering these will not only speed up your problem-solving but also give you that extra boost of confidence when you’re tackling the Quant section on test day.
The real trick here? Practice. It’s the secret sauce that’ll turn these concepts from confusing to comfortable. Don’t worry if it feels tricky at first—just keep practicing and applying the strategies we’ve talked about, and soon enough, you’ll start recognizing these patterns everywhere.
Here’s the thing: the more you practice, the more you’ll start seeing these problems as puzzles to solve rather than math tests to survive. Keep at it, stay consistent, and remember, it’s all part of the journey.
"The expert in anything was once a beginner." – Helen Hayes
You’ve got this! Keep working through the problems, stay positive, and before you know it, the GRE Quant section will be your new favourite thing. Best of luck—you’re ready for this!
