GRE Polygons, Circles and Cylinders

Let's learn about polygons, rectangles, triangles, circles, and cylinders!!!!

What Are Polygons?

A polygon is a closed, two-dimensional shape made up of straight lines. Each line segment forms a side, and the points where two sides meet are called vertices. Polygons can have as few as three sides (triangle) or many more (like an octagon or decagon).

Key Characteristics of Polygons:

1. Closed Shape: The sides form a closed figure.
2. Straight Lines: The edges are straight, not curved.
3. Angles: Each polygon has interior angles formed by its sides.

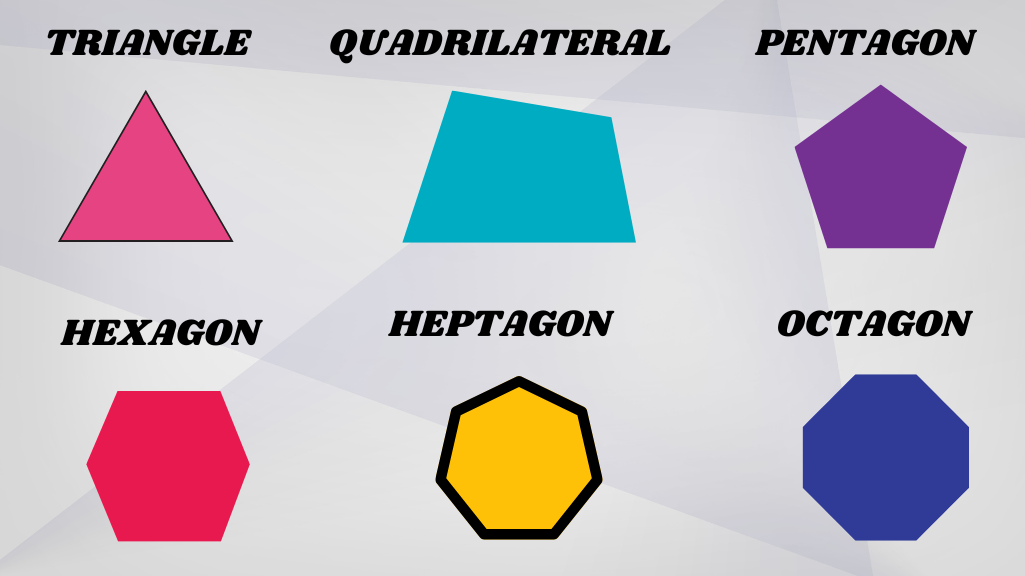
Types of Polygons by Sides

Here’s a quick breakdown of polygons based on the number of sides you might encounter on the GRE:

Properties of Polygons

Polygons are all about angles and sides. Here’s a breakdown of the essential properties you need to know for the GRE:

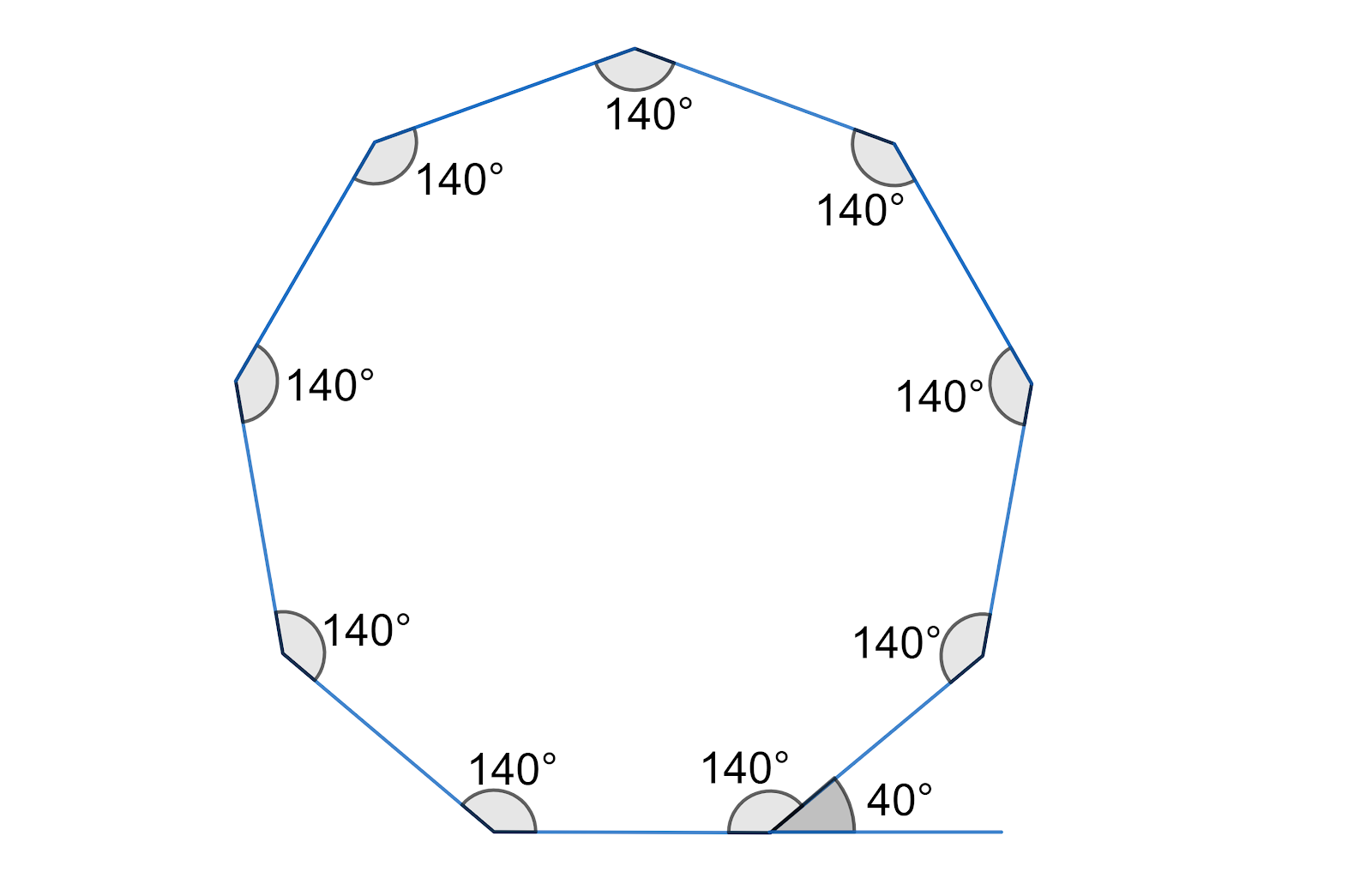
1. Interior Angles

2. Exterior Angles

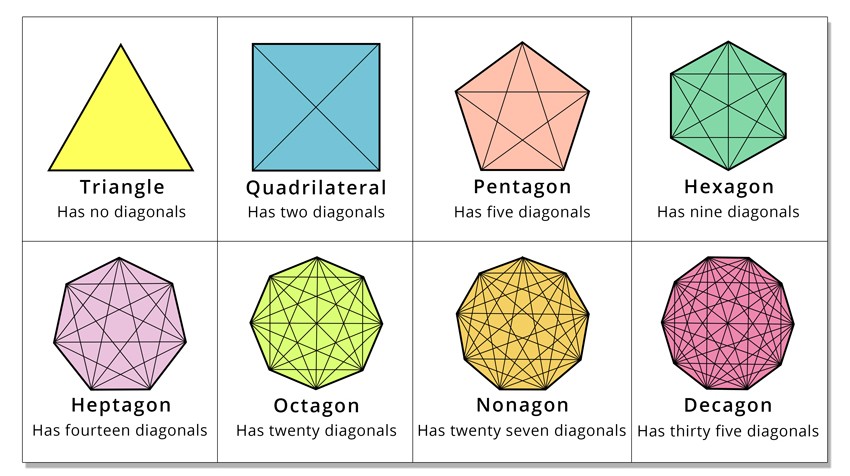
3. Diagonals

4. Regular vs. Irregular Polygons

• Regular polygons have all sides and angles equal. Examples: equilateral triangle, square, regular pentagon.
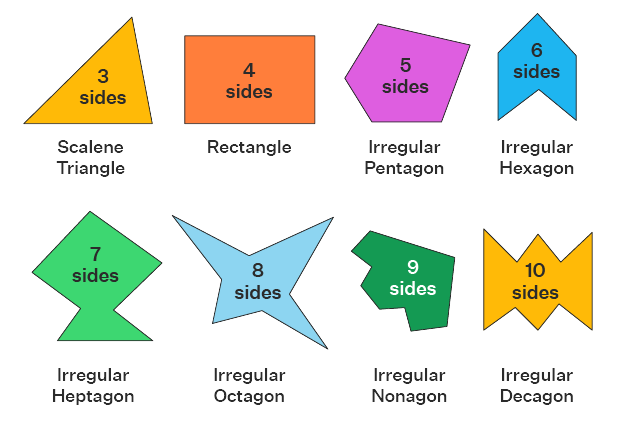
• Irregular polygons have sides and angles of varying lengths and measures.

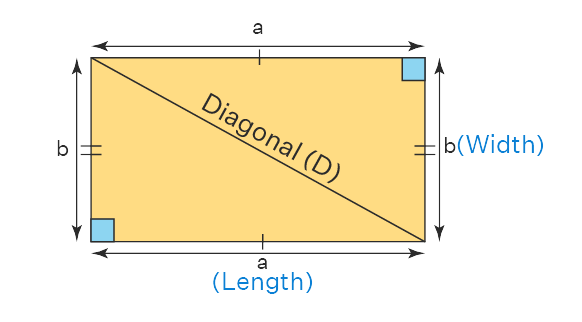
Polygons Examples:

Question 1:

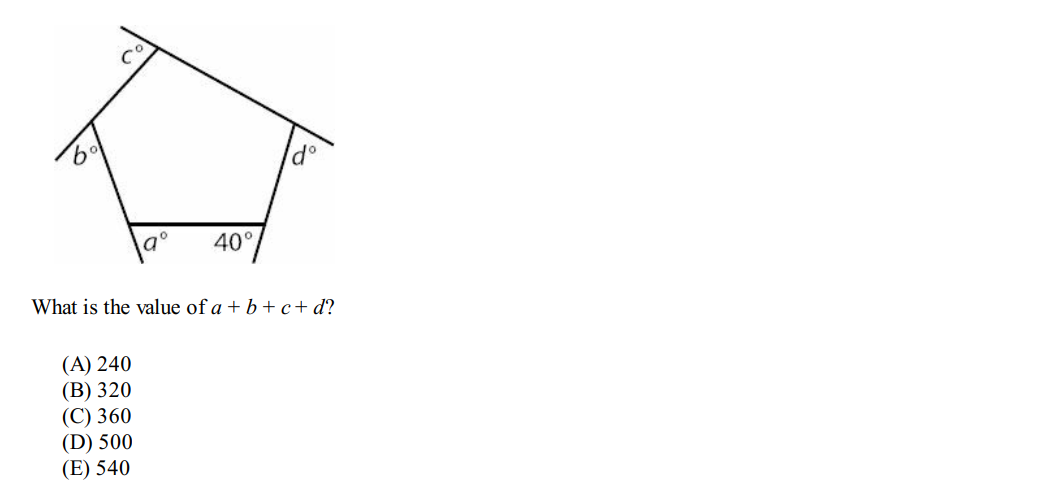
Solution:

Question 2:

Solution:

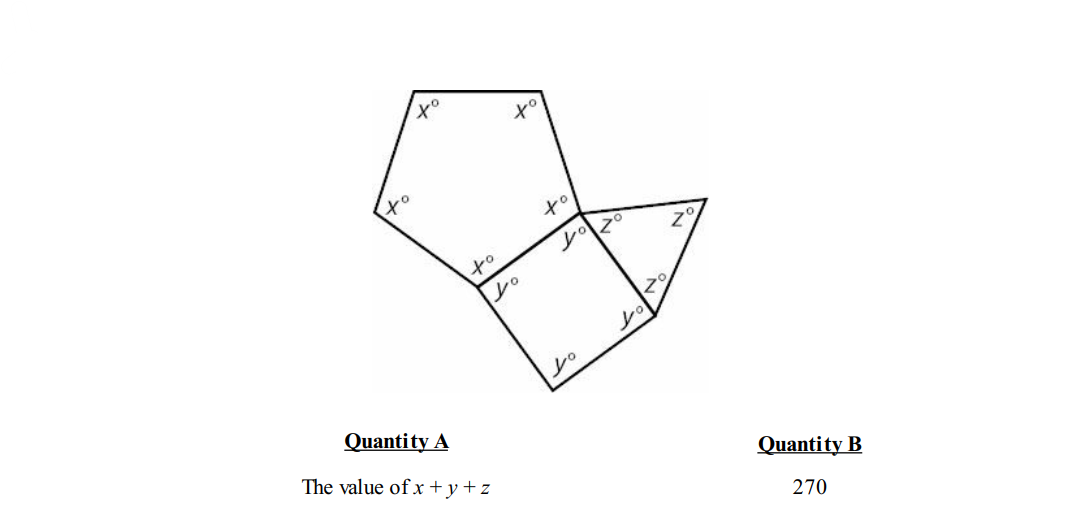
Question 3:

Solution:

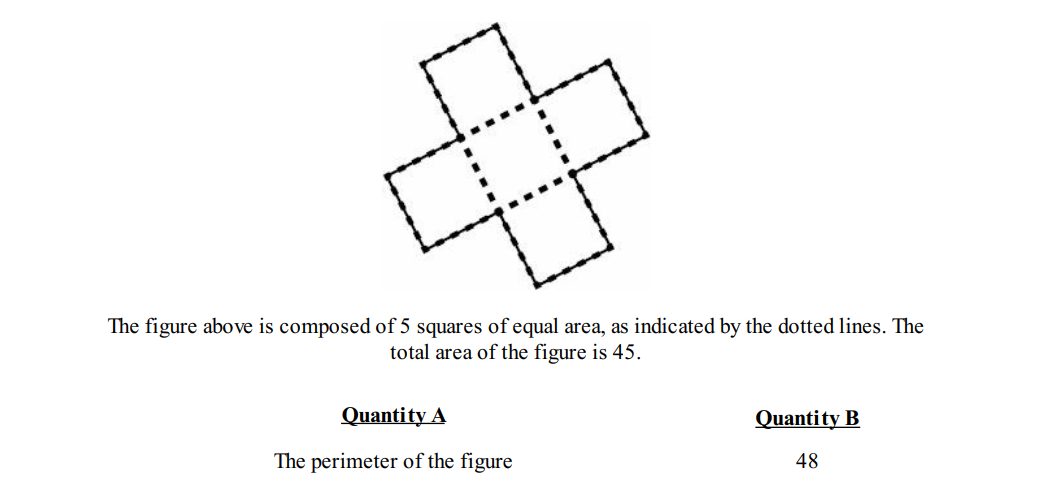
Question 4:

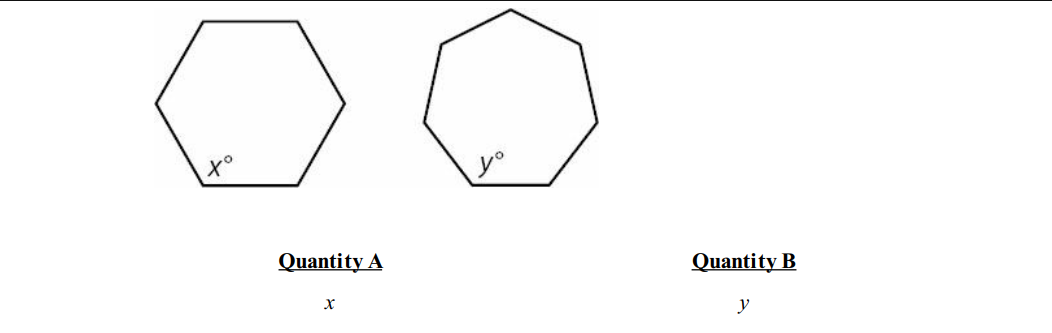
Solution:

What Is a Rectangle?

A rectangle is a quadrilateral (a polygon with four sides) where:

1. Opposite sides are equal and parallel.
2. All interior angles are 90 degrees.

Key Characteristics of a Rectangle:

• Length (l): The longer side.
• Width (w): The shorter side.
• Diagonals: The two diagonals of a rectangle are equal in length and bisect each other.

Key Properties of Rectangles

To ace rectangle-related GRE problems, familiarize yourself with these properties:

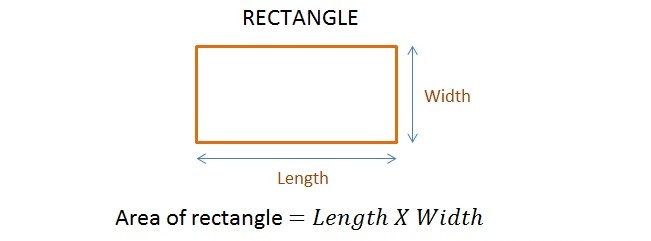
1. Area

The area of a rectangle is calculated using the formula:

Area=l×w

Where:

• l = length
• w = width
• Example: If a rectangle has a length of 10 units and a width of 4 units:

Area=10×4=40 square Units

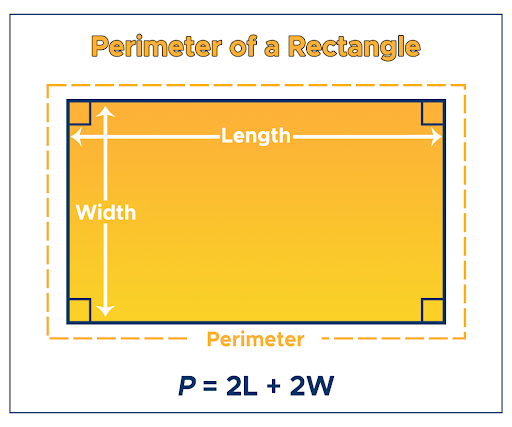
2. Perimeter

3. Diagonals

4. Symmetry

Rectangles are highly symmetric. They:

• Have two lines of symmetry, along the length and width.
• Are rotationally symmetric at 180 degrees.

Special Types of Rectangles

1. Square:
2. Golden Rectangle:
   A rectangle is considered a golden rectangle if the ratio of its length to its width is the golden ratio (≈1.618).

Rectangle Examples:

Question 1:

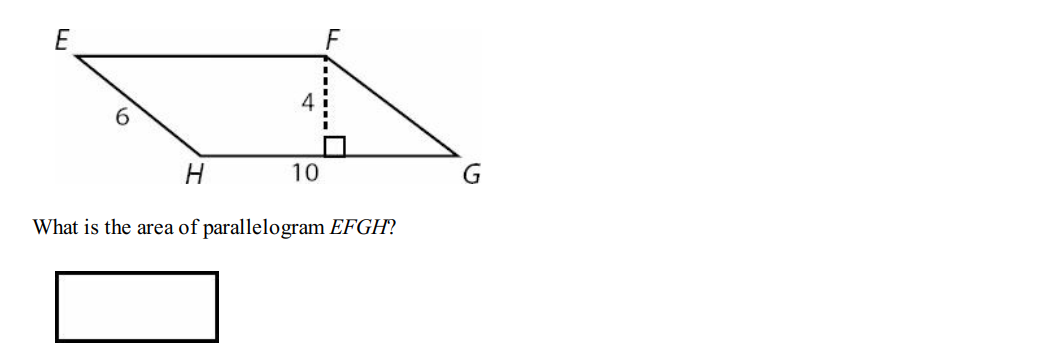
Solution:

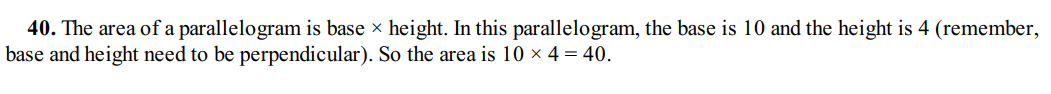
Question 2:

Solution:

Question 3:

Solution:

Question 4:

Solution:

What Is a Triangle?

A triangle is a three-sided polygon formed by connecting three line segments at their endpoints. It has three edges (sides) and three vertices (corners).

Fundamental Properties:

1. Sum of Interior Angles: The sum of the interior angles of any triangle is always 180 degrees∘.
2. Triangle Inequality Theorem: The length of any one side must be less than the sum of the other two sides and greater than their difference. 

∣a−b∣<c<a+b, |a - b| < c < a + b, ∣a−b∣<c<a+b

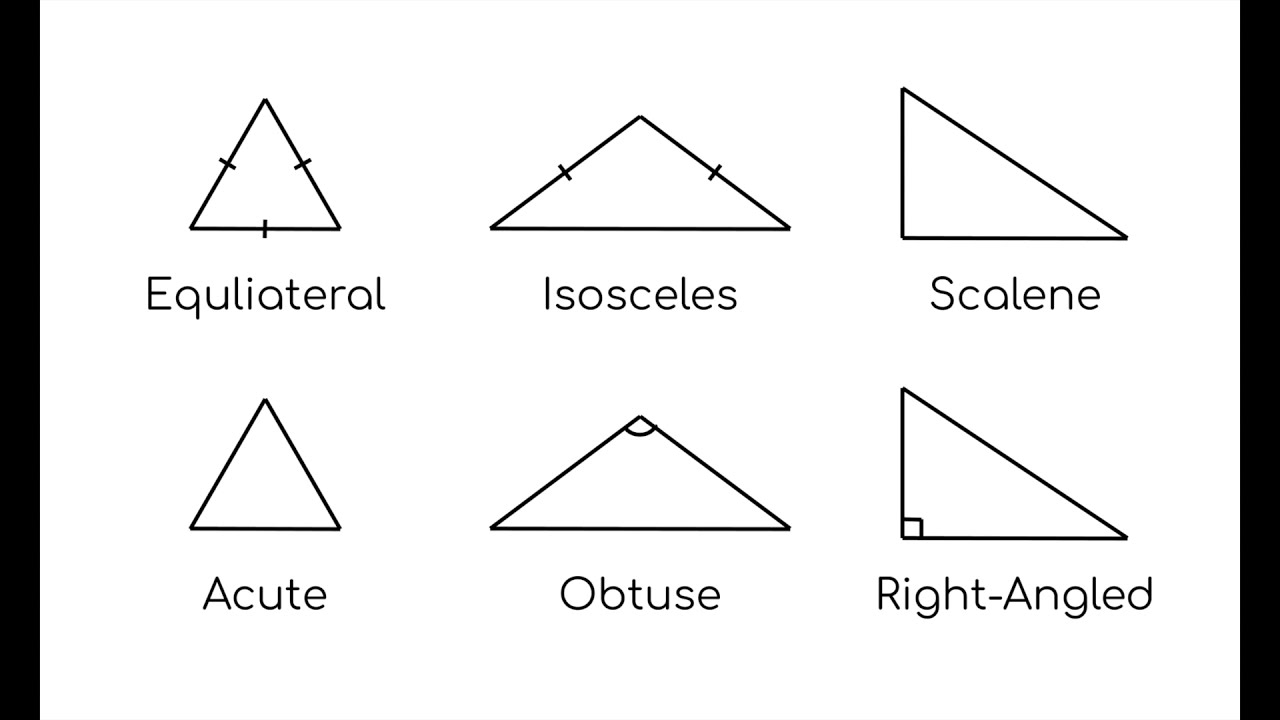
Types of Triangles

Triangles can be classified based on their angles and sides. Understanding these distinctions is essential for identifying the correct approach to solving GRE problems.

Classification Based on Angles

1. Acute Triangle: All three angles are less than 90°.
   • Examples: 60°,70°,50°
2. Right Triangle: One angle is exactly 90∘°.
   • Examples: 90°,45°,45°
   • Key property: The Pythagorean theorem applies.
3. Obtuse Triangle: One angle is greater than 90°.
   • Examples: 120°, 40°, 20°

Classification Based on Sides

1. Equilateral Triangle: All three sides are equal, and all three angles measure 60°.
   • Area formula:
2. Isosceles Triangle: Two sides are equal, and the angles opposite those sides are also equal.
3. Scalene Triangle: All sides and angles are different.

Properties and Formulas

1. Area of a Triangle

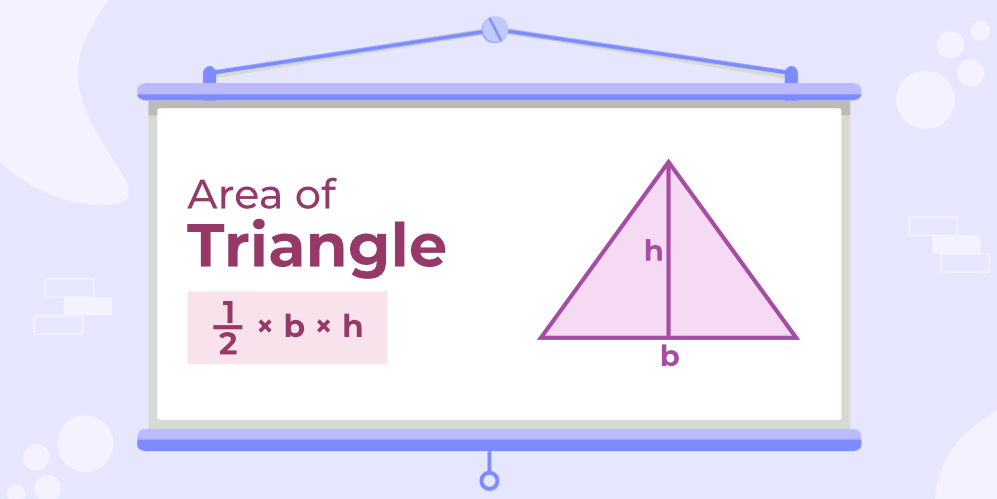
2. Perimeter of a Triangle

The perimeter is the sum of the lengths of all three sides:

                               Perimeter=a+b+c

3. Pythagorean Theorem (For Right Triangles Only)

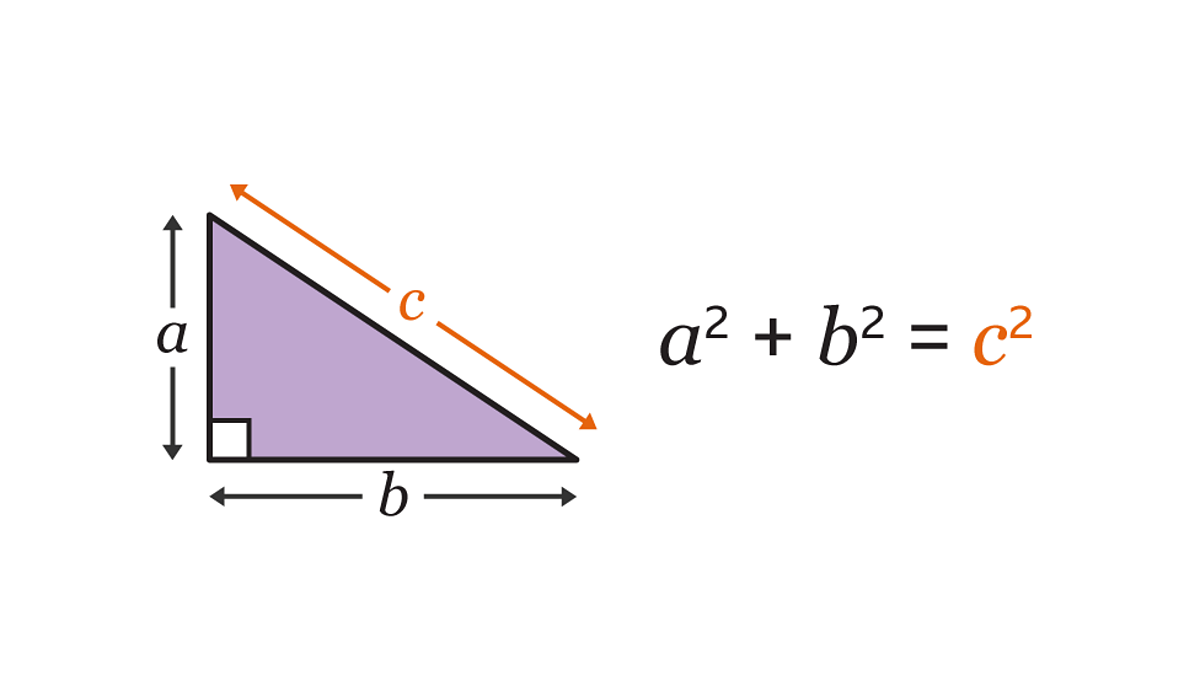
Where:

• c is the hypotenuse (the longest side).
• a and b are the two shorter sides.

4. Special Right Triangles

These appear frequently on the GRE, so memorize their properties:

a) 45°-45°-90° Triangle

• Two sides are equal.
• Hypotenuse = s2, where s is the length of each leg.
• Example: If the legs are 5, the hypotenuse is 52​.

b) 30°-60°-90° Triangle

• The sides are in the ratio 1: root(3)

5. Triangle Inequality Theorem

The sum of the lengths of any two sides must be greater than the length of the third side.

6. Sum of Interior Angles

The total measure of the three interior angles is always 180 degrees.

7. Exterior Angle Theorem

The measure of an exterior angle equals the sum of the two non-adjacent interior angles:

Exterior Angle=Angle1+Angle2 

Triangle Examples:

Question 1:

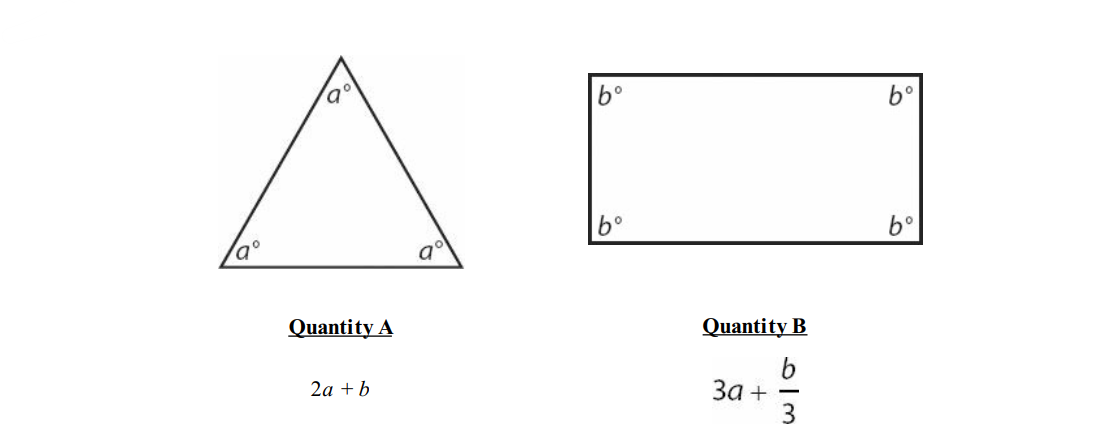
Solution:

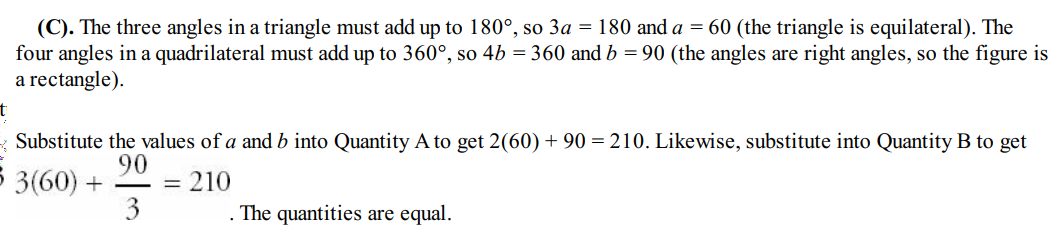
Question 2:

Solution:

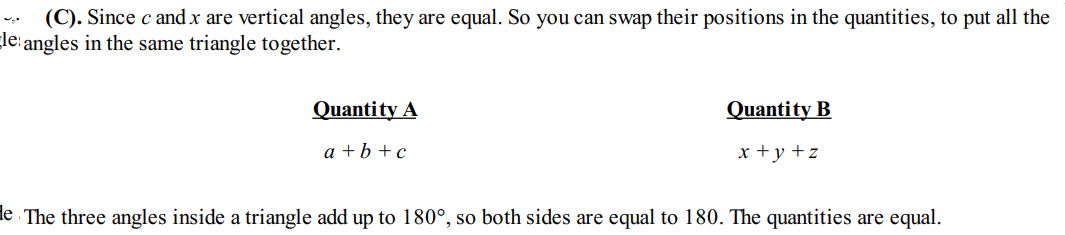
Question 3:

Solution:

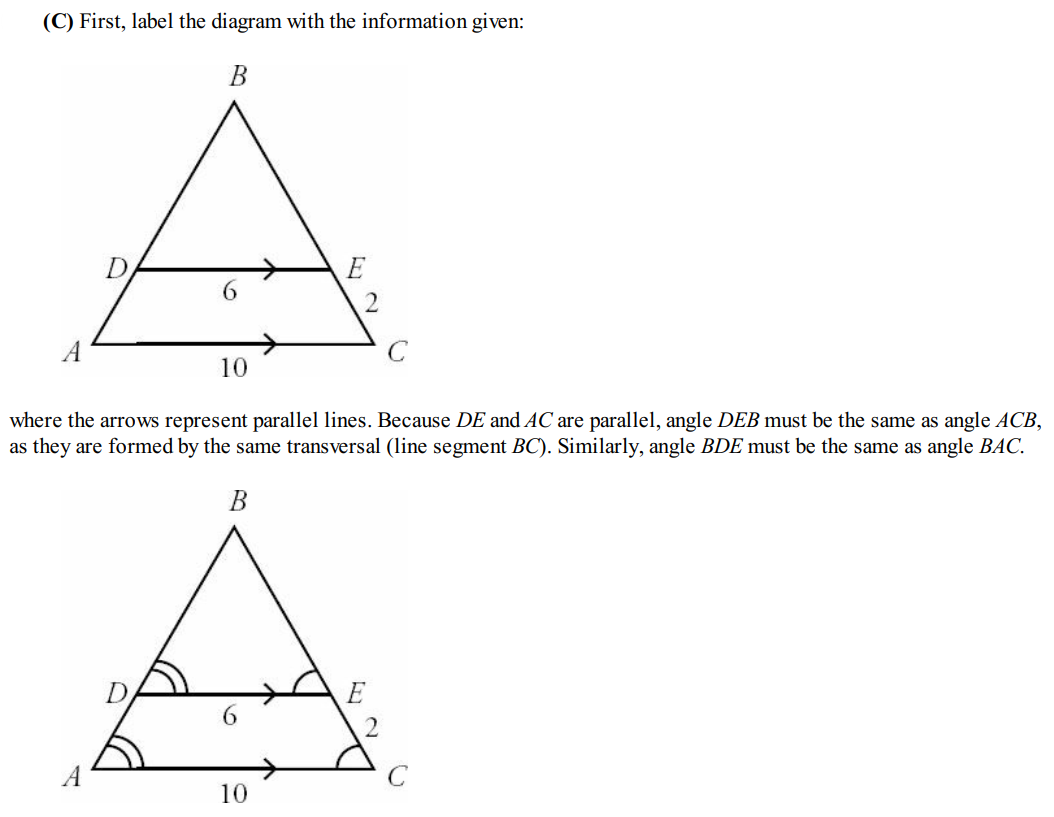
Question 4:

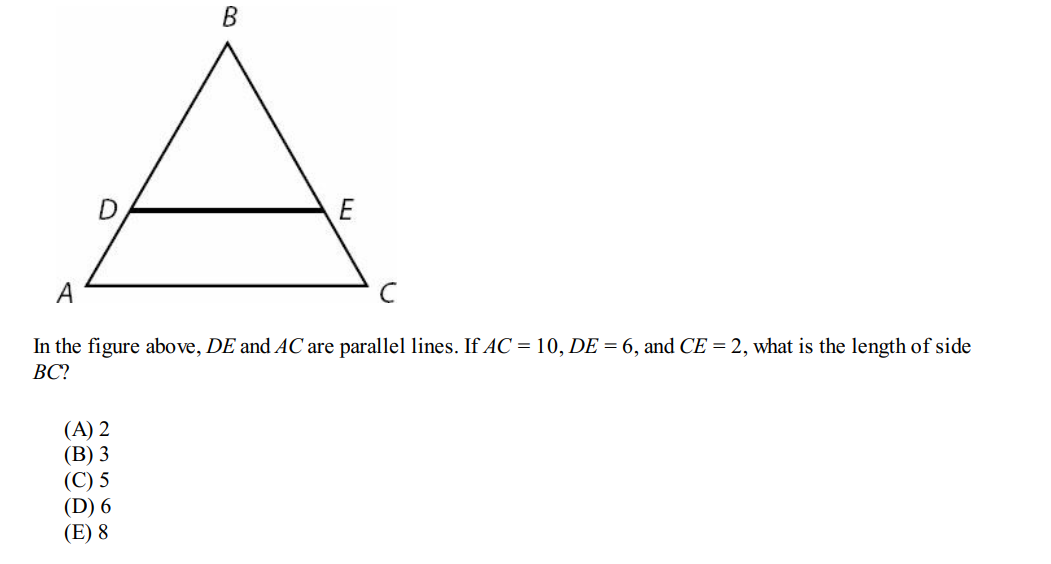
Solution:

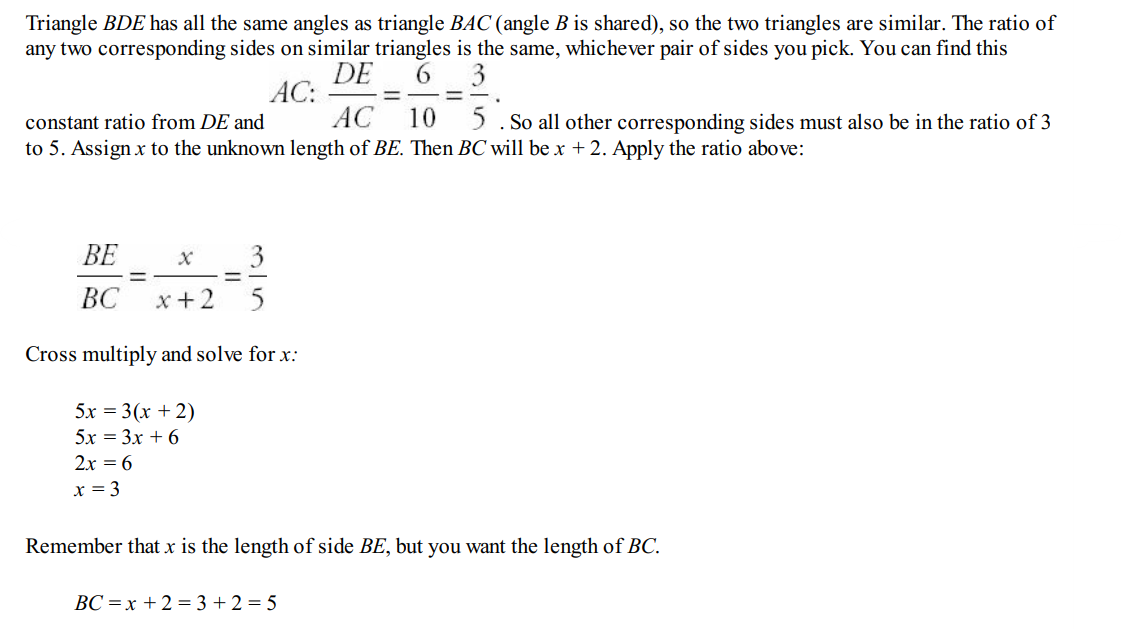
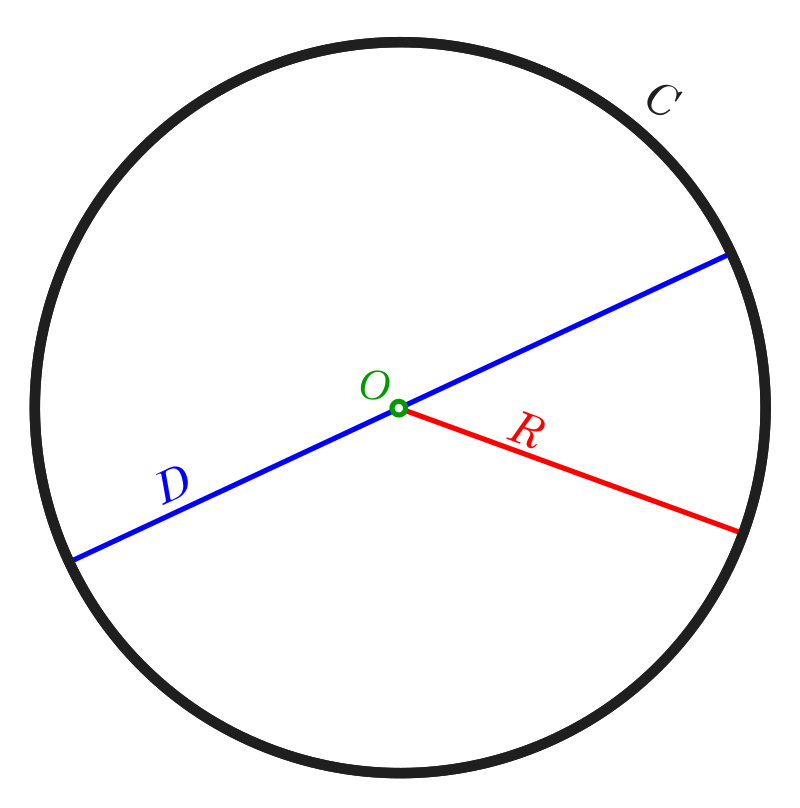
What Is a Circle?

A circle is a two-dimensional geometric shape consisting of all points that are equidistant from a fixed point, called the center.

Key Components:

1. Radius (r): The distance from the center to any point on the circle.
2. Diameter (d): The distance across the circle, passing through the center. It is twice the radius: d=2rd = 2rd=2r
3. Circumference (C): The total distance around the circle.
4. Chord: A line segment whose endpoints lie on the circle.
5. Arc: A portion of the circle's circumference.
6. Sector: A region bounded by two radii and the intercepted arc.
7. Tangent: A line that touches the circle at exactly one point.
8. Central Angle: An angle whose vertex is at the center of the circle and whose sides are radii.

Important Properties and Formulas

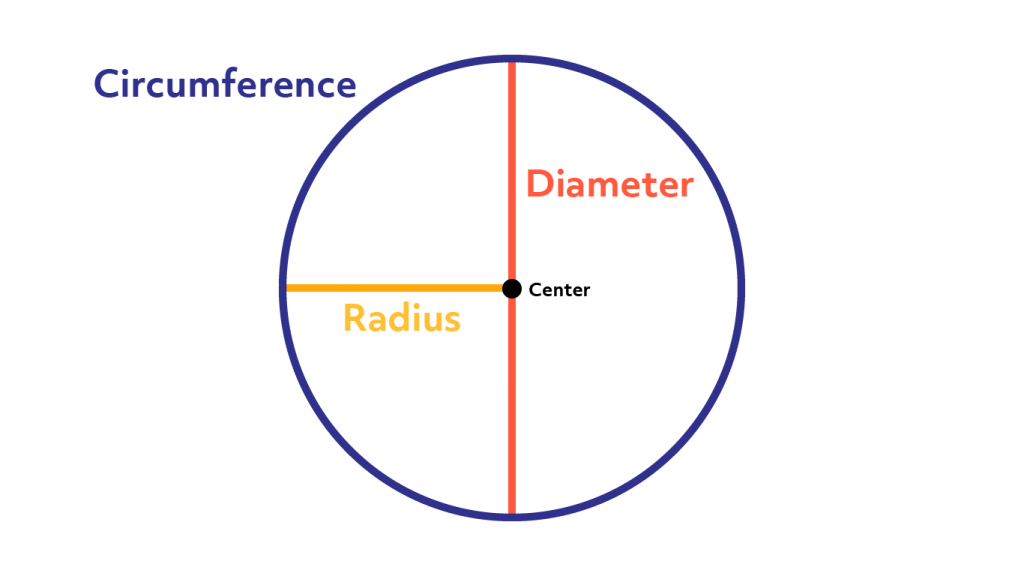
1. Circumference

The circumference is the total distance around the circle, calculated as:

C=2πr or C=πd

2. Area of a Circle

The area enclosed by a circle is given by:

Area=πr^2

3. Arc Length

The length of an arc is the fraction of the circle's circumference corresponding to the central angle:

Arc Length=θ/360°×2πr

Where θ is the central angle in degrees.
 

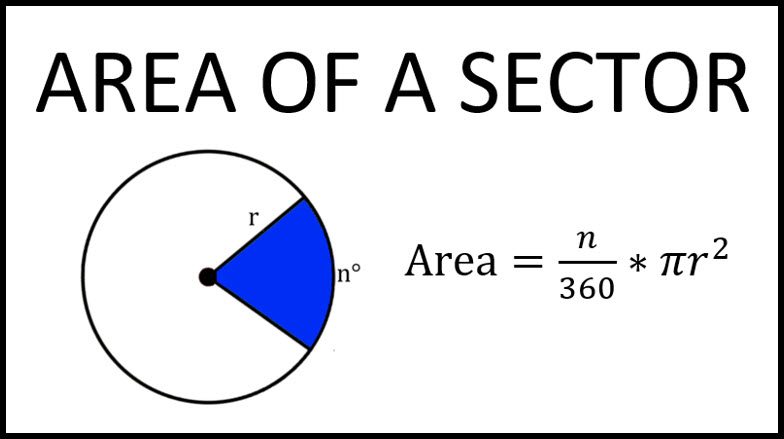
4. Area of a Sector

The area of a sector (a "slice" of the circle) is:

Sector Area=θ/360°×πr^2

5. Equation of a Circle (Coordinate Geometry)

In the coordinate plane, the equation of a circle with center (h,k)(h, k)(h,k) and radius r is:

(x−h)^2+(y−k)^2=  r^2

For a circle centered at the origin (0,0)(0, 0)(0,0), the equation simplifies to:

x^2+y^2=  r^2

6. Tangent to a Circle

A tangent to a circle is perpendicular to the radius at the point of contact.

Circle Examples:

Question 1:

Solution:

Question 2:

Solution:

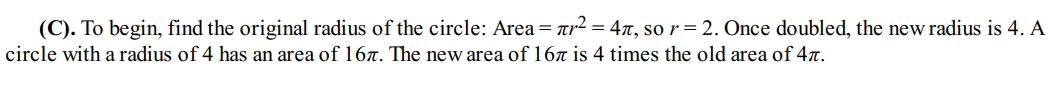
Question 3:

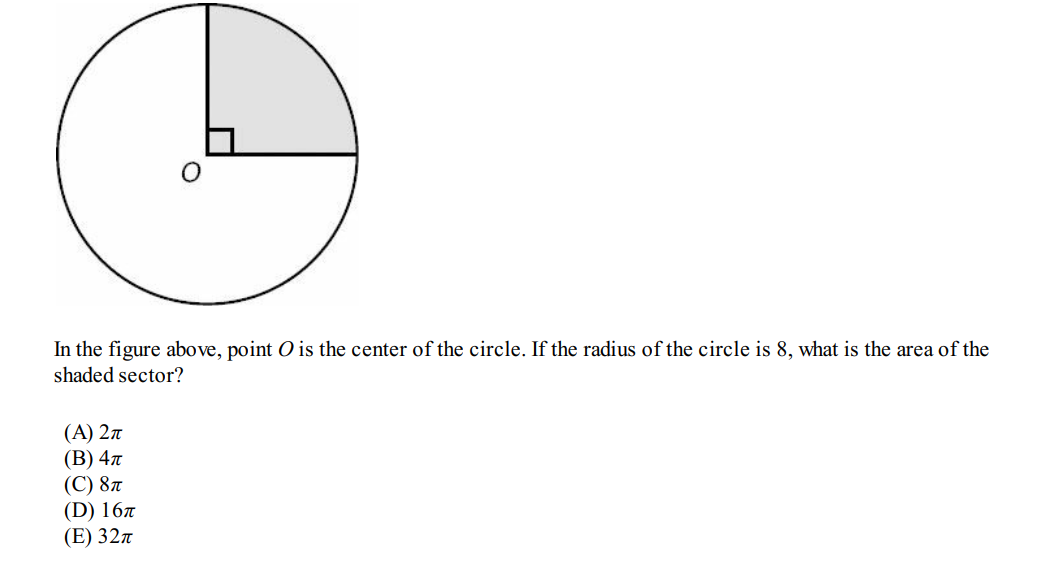
Solution:

Question 4:

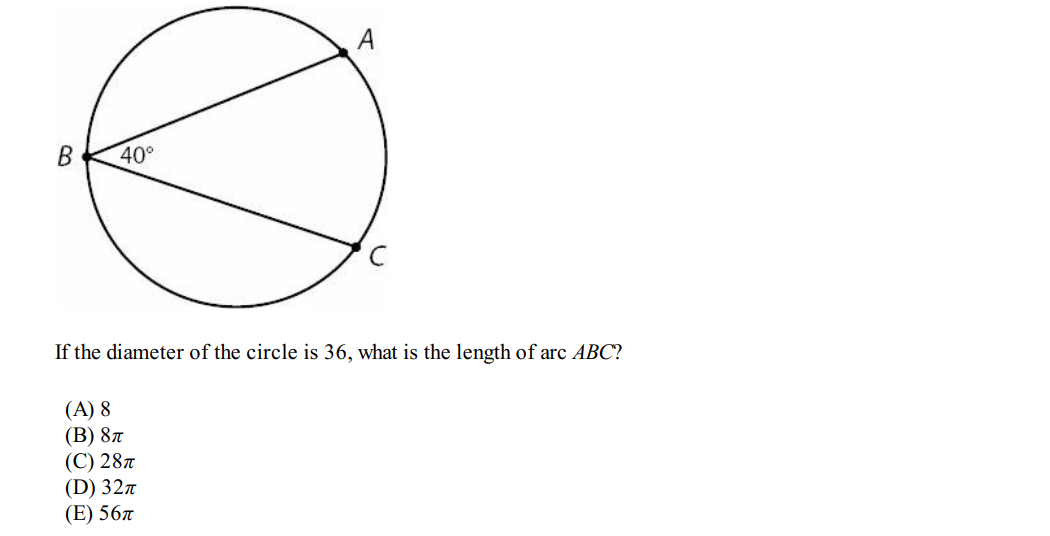
Solution:

What Is a Cylinder?

A cylinder is a 3D geometric shape with two parallel, congruent circular bases connected by a curved surface. It resembles a can or a tube. Cylinders are classified as right cylinders when the sides are perpendicular to the bases (most common on the GRE) or oblique cylinders when the sides are slanted.

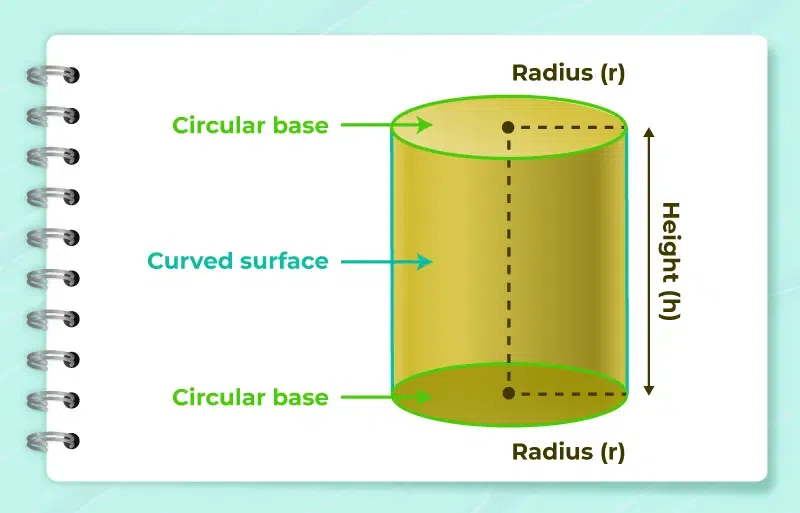
Key Components of a Cylinder

1. Radius (r): The radius of the circular base.
2. Height (h): The perpendicular distance between the two bases.
3. Base Area (A): The area of the circular base, calculated as: 

1. Lateral Surface Area: The curved surface connecting the two bases.
2. Total Surface Area: The sum of the areas of the lateral surface and the two bases.
3. Volume (V): The space enclosed within the cylinder.

Important Formulas for Cylinders

1. Volume of a Cylinder

The volume is the product of the base area and the height:

2. Lateral Surface Area

The lateral surface area is the area of the curved surface, given by:

Lateral Surface Area = 2πrh

3. Total Surface Area

The total surface area includes the lateral surface area and the areas of the two circular bases:

Cylinder Examples:

Question 1:

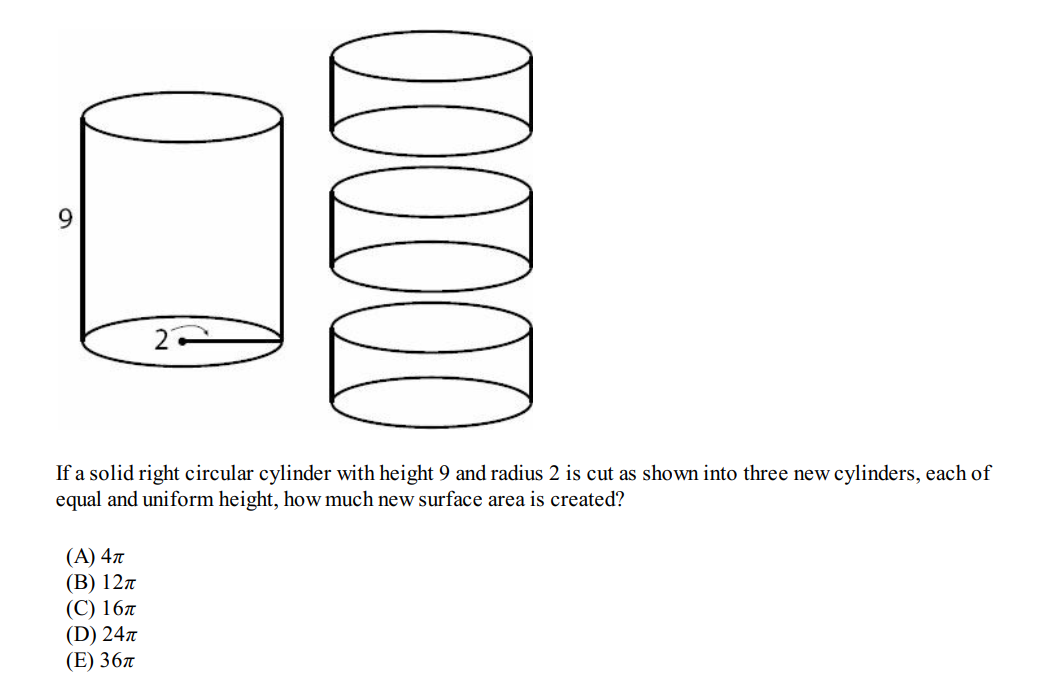
Solution:

Question 2:

Solution:

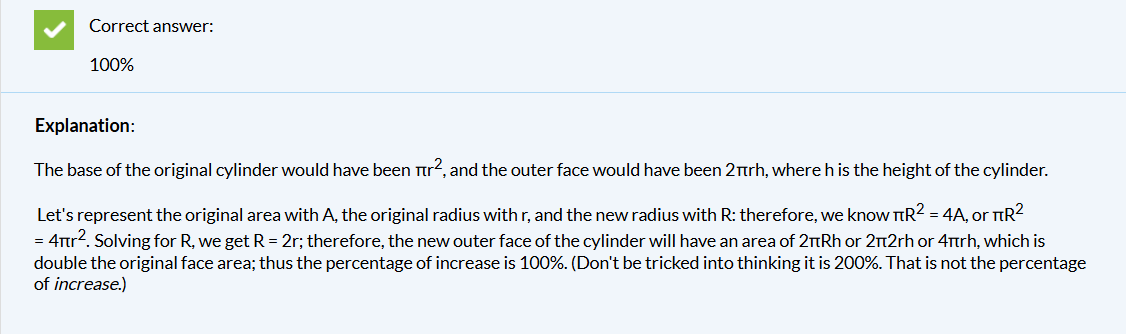
Question 3:

Solution:

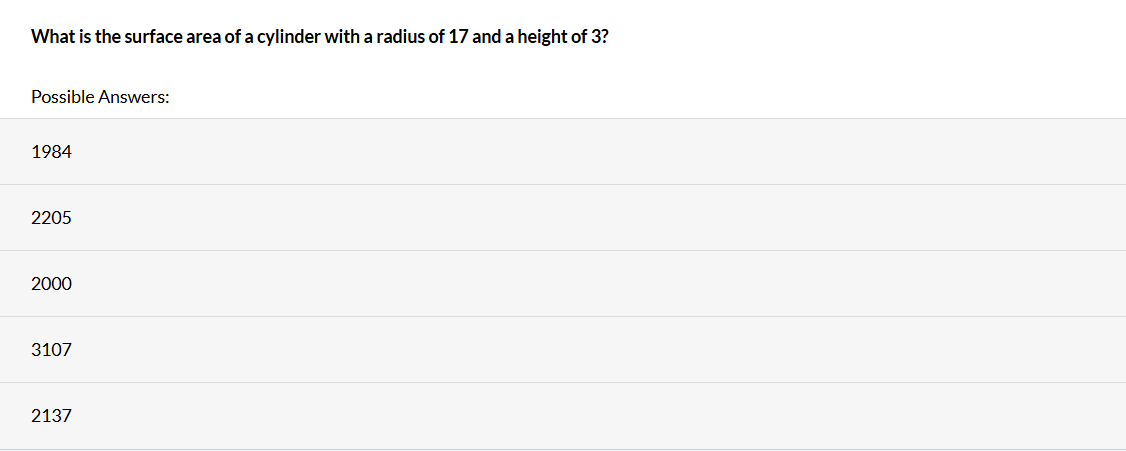
Question 4:

Solution: