Introduction
Okay, let’s be honest—no one really looks forward to the GRE Quant section, but it’s definitely something you can tackle with the right mindset and tools. And guess what? Ratios, averages, median, and mode are like your trusty toolkit for getting through the math part without too much drama. These concepts pop up a lot, and once you understand them, you’ll feel a lot more confident when you see them on the test.
Here’s the deal: ratios, averages, median, and mode show up in a big chunk of the GRE Quant section. Ratios make an appearance in about 10-15% of the questions, averages in about 12-18%, and median and mode pop up around 8-12%. While it may not seem like a huge percentage individually, when you put them all together, it’s a lot of ground to cover, so getting comfortable with them will pay off big time.
Now let’s break it down a bit. Ratios are all about comparing things. For example, if you're trying to figure out how many pizzas you need to order for a group of friends, ratios help you solve that problem quickly (no one likes running out of pizza). Averages help you figure out the “typical” or “middle” value in a set of numbers—think of it like finding the average of your weekly grocery bill. Median is just the middle number in a set, while mode is the number that shows up the most. So, if you’re trying to decide which ice cream flavor is the most popular at a party, mode can help you figure that out.
But the key isn’t just memorizing formulas—it’s knowing how to spot these problems and solving them fast. Don’t worry, though—we’ve got your back! In this guide, we’ll walk you through each concept, explain how they work, and share some tips and practice problems to help you get comfortable. With these tools in hand, you’ll feel way more ready to take on the GRE Quant section with confidence (and maybe even enjoy it a little). Let’s jump in and make these numbers work for you!
"The only way to learn mathematics is to do mathematics." — Paul Halmos
Ratios
Short Note
Ratios are just the comparison between two or more things, usually written in a form like a:b or a/b. This is essentially the law of proportions—what happens to one thing when another thing changes. It's like that time you mixed 3 parts juice to 2 parts water, and everything magically tasted perfect!
The Law of Calculation for Ratios:
- If you have a ratio a:b and you’re asked to find the missing values, the general rule is:
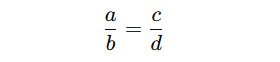
- Meaning: cross-multiply! So, if a:b = c:d, then a × d = b × c. Just like two slices of pizza being equally split between two friends—if you cross-multiply, you keep everything fair and square.
Tip:
When you get a ratio question, treat it like a recipe. If you're given ingredients (numbers), just mix them in the right proportion! Stay calm and remember: ratios aren’t as scary as they sound, they’re just math recipes waiting to be solved. Keep the proportions balanced, and you’ll be the pizza-maker of the GRE!
Example with Step by Step Solution
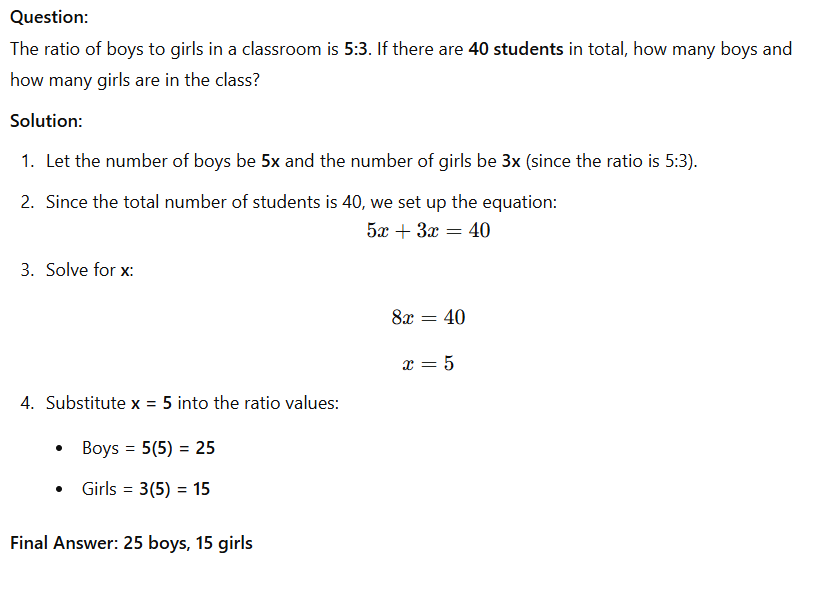
Average
Short Note
An average is like the middle ground—it takes everything in a group, puts it all together, and averages out the drama. Whether you’re averaging out your weekly grocery bills or calculating your friend group’s movie ratings, averages help you find a balance in all the numbers.
The Law of Calculation for Averages:
- The formula for an average is:
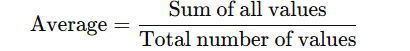
Essentially, you're summing all the numbers and then dividing by how many numbers there are. So, if you want the average of 5, 10, 15, just add them up (5 + 10 + 15 = 30) and divide by 3 (since there are 3 numbers). 30 ÷ 3 = 10. Boom, the average is 10!
Example with Step by Step Solution

Median
Short Note
The median is the number that splits the data right down the middle. If you have an odd number of values, it’s the one right in the center. If you have an even number of values, it’s the average of the two middle values.
The Law of Calculation for Median:
- To find the median, first arrange the numbers in ascending or descending order. Then, if there are odd numbers of data, pick the middle one. If there are even numbers of data, average the two middle ones. Example: For 5, 10, 12, 18, 22, the middle value is 12. For 7, 9, 10, 15, the middle values are 9 and 10, so the median is:
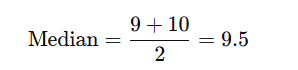
Example with Step by Step Solution
Question:
Find the median of the following set of numbers: 12, 18, 5, 22, 30, 25, 10.
Solution:
- Arrange the numbers in ascending order: 5,10,12,18,22,25,305, 10, 12, 18, 22, 25, 305,10,12,18,22,25,30
- Since there are 7 numbers (an odd count), the median is the middle number.
- The middle number (4th in the list) is 18.
Final Answer: 18
Mode
Short Note
The mode is the number that shows up the most often. It’s the repeat champion of the set, the MVP who just can’t seem to leave the spotlight. In a crowd of numbers, the mode is the loudest one, demanding attention!
The Law of Calculation for Mode:
- To find the mode, simply count the occurrences of each number in the data set. The number that appears most often is the mode. If more than one number appears most often, you have a bimodal (or even multimodal) distribution. If no number repeats, there is no mode. Example: In the set 7, 9, 9, 10, 15, the mode is 9 because it appears the most.
Tip:
The mode is like the party animal of numbers—it’s the one that’s always there, showing up the most and grabbing all the attention. If you're ever in doubt, just ask yourself: Who’s making the most noise in this group? That’s your mode! And trust me, it’s there to help you out in any data set—just follow the noise!
Example with Step by Step Solution
Question:
Find the mode of the following set of numbers: 7, 12, 15, 12, 18, 12, 9, 15, 9, 9.
Solution:
Count the occurrences of each number:
- 7 appears once
- 12 appears three times
- 15 appears twice
- 18 appears once
- 9 appears three times
The mode is the number that appears the most frequently.
Since 12 and 9 both appear three times, this dataset has two modes (bimodal distribution).
Final Answer: 12 and 9
Some GRE Problems with Step by Step Solutions
Question 1

Solution:

Question 2
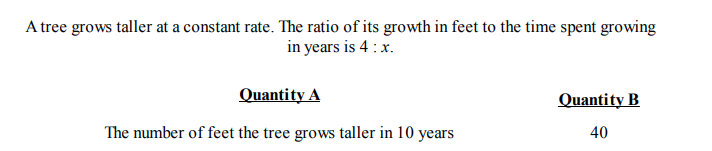
Solution:
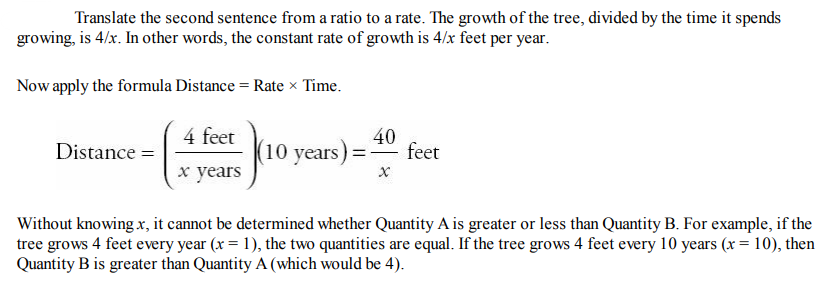
Question 3

Solution:

Question 4
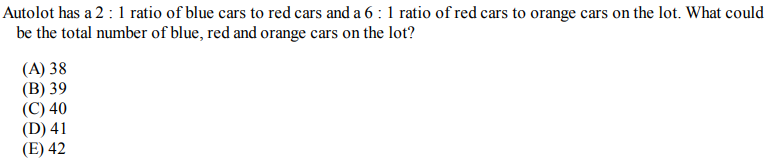
Solution:

Question 5

Solution:

Question 6

Solution:

Question 7
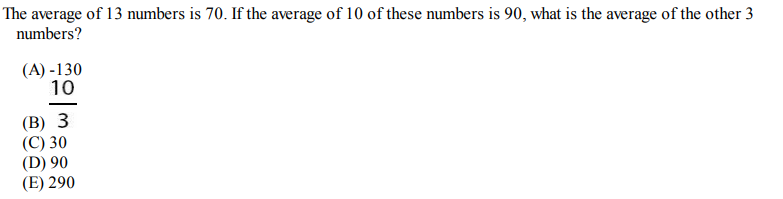
Solution:

Question 8

Solution:

Question 9
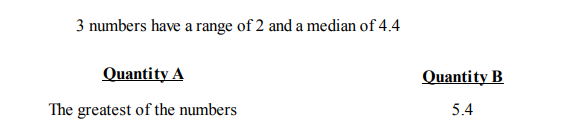
Solution:

Question 10

Solution:

Conclusion
We’ve walked through the core GRE Quant concepts—ratios, averages, median, and mode—and how each one plays a big role in solving problems quickly and accurately. These concepts may seem simple at first glance, but mastering them can make all the difference when it comes to acing the GRE. Whether you’re comparing quantities with ratios, finding trends with averages, or analyzing data with median and mode, these tools will help you approach questions with confidence.
But here’s the real truth: practice is where the magic happens. It’s not enough to just read through the material—you’ve got to put it into action. The more you practice, the more natural it’ll feel to solve problems on the spot. Don’t hesitate to lean on study resources—practice tests, study guides, or even online video tutorials—and stay consistent with your prep. Little by little, you’ll find yourself getting faster and more accurate, and you’ll be ready for anything the GRE throws your way.
As you continue preparing, remember that this is just one step on the road to your bigger dreams. Keep at it, stay focused, and don’t be afraid to ask for help when you need it. You’re getting closer to your goal every day, and the hard work you put in now will pay off.
You’ve got this—one question at a time, and you’re on your way to success!
"Success is the sum of small efforts, repeated day in and day out." — Robert Collier
This quote perfectly captures the power of consistent practice. Every small effort adds up, and soon enough, you’ll see the results. Keep going, you’re on the right track!
