Introduction
Let’s be honest—when you hear “Quantitative Reasoning,” it doesn’t exactly scream excitement, right? But here’s the thing: the Quant section of the GRE makes up half of your total score. So, yeah, it’s kind of a big deal.
Here’s a little secret: most test-takers find topics like functions, formulas, and number properties tricky. The good news? If you can master these, you’ll already be ahead of the pack. Think of it like learning the cheat codes to a video game—you’ll solve problems faster and with way less stress.
In this blog, we’ll break down these concepts into simple, easy-to-understand chunks. No fancy math jargon, just clear explanations, tips, and strategies to help you handle any question the GRE throws your way. Ready to crush it? Let’s get started!
"Mathematics is not about numbers, equations, computations, or algorithms: it is about understanding." – William Paul Thurston
Even and Odd Numbers
Short Notes
Understanding even and odd numbers is like understanding the basic rules of a game. If you know the rules, the game gets a lot easier! Here’s the breakdown:
- Even numbers are those divisible by 2, like 2,4,6,8 and so on. The moment you see a 2 at the end, it’s even.
- Odd numbers leave a little “leftover” when divided by 2, like 1,3,5,7 and so on. You can tell they're odd by their unpredictable behaviour (just like some of us on a Monday morning!).
The Law of Calculation:
- Addition/Subtraction:
- Even + Even = Even
- Odd + Odd = Even
- Even + Odd = Odd
- Multiplication:
- Even × Anything = Even
- Odd × Odd = Odd
Tips:
- When dealing with even and odd numbers in equations, think of it like a dance: they always have their partners, and if the rhythm is wrong (like even + odd), things get messy!
- Trick to Remember: Whenever you see an "even" number in a problem, mentally high-five yourself because it’s the easiest to work with.
Example with Step by Step Solution


Which of the following numbers is divisible by 6?
(A) 342
(B) 421
(C) 537
(D) 216
Solution:
A number is divisible by 6 if it is divisible by both 2 and 3.
- Divisibility by 2: A number is divisible by 2 if its last digit is even.
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is a multiple of 3.
Checking each option:
- 342: Last digit is 2 (even) ✅, Sum = 3+4+2 = 9 (divisible by 3) ✅ → Divisible by 6
- 421: Last digit is 1 (not even) ❌ → Not divisible by 6
- 537: Last digit is 7 (not even) ❌ → Not divisible by 6
- 216: Last digit is 6 (even) ✅, Sum = 2+1+6 = 9 (divisible by 3) ✅ → Divisible by 6
Correct answers: (A) 342 and (D) 216
Divisibility Rules
Short Notes
The divisibility rules are like shortcuts in a maze—they help you find the fastest path to the answer! Let’s break down some key divisibility rules:
- Divisible by 2: A number is divisible by 2 if it ends in 0, 2, 4, 6, or 8 (the classic even-number rule).
- Divisible by 3: If the sum of the digits of a number is divisible by 3, then the number itself is divisible by 3.
- Divisible by 5: A number is divisible by 5 if it ends in either 0 or 5.
- Divisible by 7: For 7, just double the last digit, subtract it from the rest of the number, and if the result is divisible by 7, you’re golden!
The Law of Calculation:
- Divisibility rules simplify your life by eliminating options and saving time. Instead of manually dividing each number, these rules help you make quick decisions on what’s possible.
Tips:
- Visualize the process: As soon as you see a number, mentally check if it fits the divisibility rule. It’s like playing Sudoku—get good at checking and eliminating!
- Practice with a twist: Try making a game of divisibility—every time you spot a number divisible by 5, take a “math break” (or a dance break—your choice).
Example with Step by Step Solution
Which of the following numbers is divisible by 6?
(A) 342
(B) 421
(C) 537
(D) 216
Solution:
A number is divisible by 6 if it is divisible by both 2 and 3.
- Divisibility by 2: A number is divisible by 2 if its last digit is even.
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is a multiple of 3.
Checking each option:
- 342: Last digit is 2 (even) ✅, Sum = 3+4+2 = 9 (divisible by 3) ✅ → Divisible by 6
- 421: Last digit is 1 (not even) ❌ → Not divisible by 6
- 537: Last digit is 7 (not even) ❌ → Not divisible by 6
- 216: Last digit is 6 (even) ✅, Sum = 2+1+6 = 9 (divisible by 3) ✅ → Divisible by 6
Correct answers: (A) 342 and (D) 216
Evaluating a Function
Short Notes

Example with Step by Step Solution
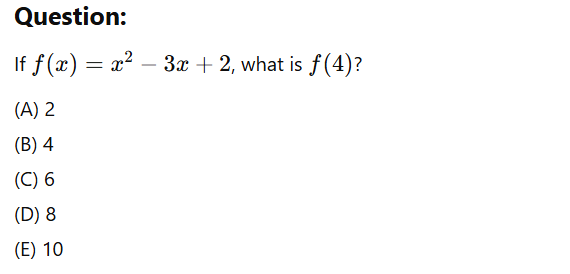

GCD and LCM
Short Notes
The Greatest Common Divisor (GCD) and Least Common Multiple (LCM) are your BFFs when it comes to solving problems with fractions, ratios, and shared schedules! Here’s the breakdown:
- GCD: It’s the largest number that divides two numbers. Imagine finding the biggest puzzle piece that fits into both puzzles (numbers).
- LCM: It’s the smallest number that both numbers divide into evenly. It’s like finding the smallest common ground where both numbers meet.
The Law of Calculation:
- GCD: Look for common factors between numbers, and pick the largest one.
- LCM: Multiply the highest powers of all prime factors of each number. It’s like collecting the best parts of each number and putting them together.
Tips:
- Trick to Remember GCD: Think of it as the “greatest” factor that works for both numbers. If a number can’t be evenly divided by both, it’s not in the club!
- LCM Tip: Keep your eyes peeled for multiples. If you’re hunting for an LCM, it’s like looking for a party where both numbers are invited.
Example with Step by Step Solution

Remainders and Modular Arithmetic
Short Notes
Remainders and modular arithmetic are like leftovers—what you get after you divide. When you divide a number by another, the remainder is what's left over. Modular arithmetic just gives you a shortcut to figure out those leftovers.
- For example, 37÷5=7 remainder 2, and we can say 37mod 5=237 \mod 5 = 2.
The Law of Calculation:
- Think of modular arithmetic as the art of “remainder math.” It’s all about how things divide up and what’s left behind. Remember to apply the "mod" as the remainder of division!
Tips:
- Fun Tip: Picture the remainder as a rebellious kid who doesn’t fit into the full group—he’s just "leftover," and you’re trying to figure out how much room is left!
- Practice Tip: Use modular arithmetic when you want to skip all that long division—just look for shortcuts! You'll become a remainder-solving ninja in no time.
Example with Step by Step Solution

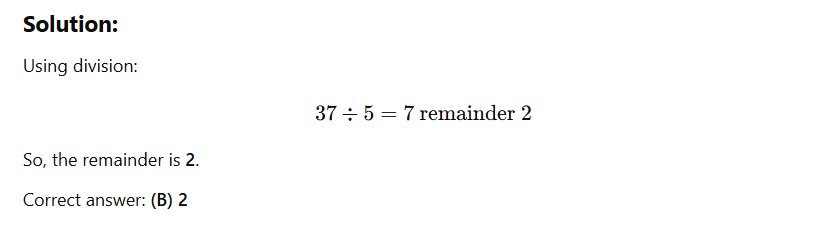
Some GRE Problems with Step by Step Solutions
Question 1
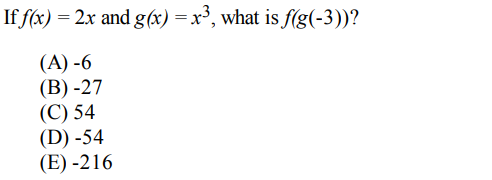
Solution:

Question 2

Solution

Question 3

Solution

Question 4

Solution:

Question 5

Solution:

Question 6
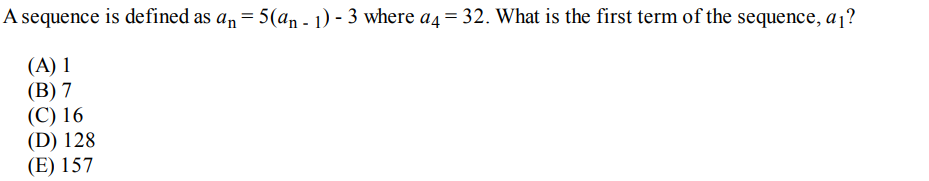
Solution:
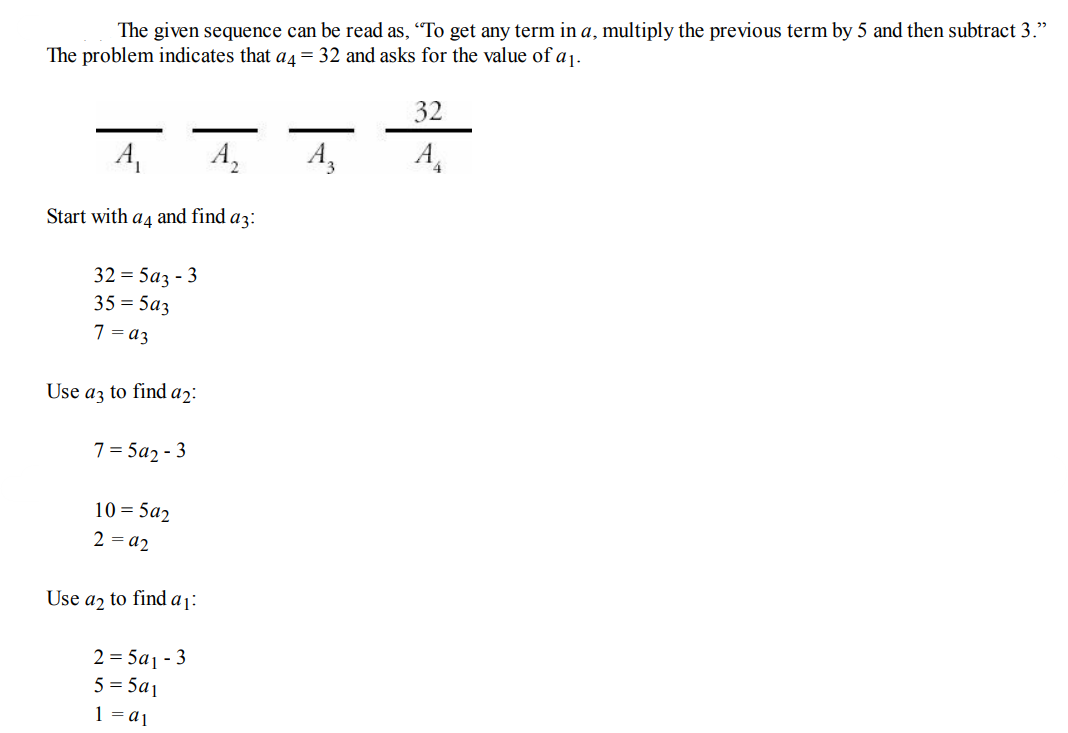
Question 7

Solution:

Question 8

Solution:

Question 9

Solution:
Since the pattern has 5 elements, find the remainder when 234 is divided by 5, which is just the units digit in this case. Alternatively, 5 goes evenly into 230, and since 234 - 230 = 4, the remainder is 4. The 4th color in the pattern, orange, is the answer.
Question 10
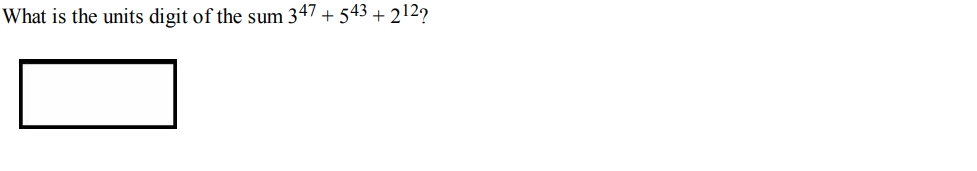
Solution:

Conclusion
Alright, here’s the truth: mastering functions, formulas, and number properties is your secret weapon for acing the GRE Quant section. These topics are like the building blocks to your GRE success. Once you get comfortable with them, solving problems becomes way less stressful (and, dare I say, kind of fun?).
Here’s a fun fact: about 70% of test-takers struggle with the basics of number properties. That means, if you get these right, you’re already in the top tier! Pretty cool, right?
But here’s the key—knowing the material is one thing, but practicing it is where the magic happens. The more you work with these concepts, the more natural they’ll feel. It’s like anything—practice makes perfect. So, keep working through problems, get comfortable with the formulas, and before you know it, the GRE will seem a lot less intimidating.
You’ve got this! Stay consistent, keep practicing, and soon enough, you’ll be walking into test day with all the confidence in the world.
"Success is the result of preparation, hard work, and learning from failure." – Colin Powell
