Alright, let’s talk about those GRE word problems. They can seem like a big headache, right? Whether you’re a math expert or you haven’t seen an algebra equation since high school, word problems can throw you off. But don’t sweat it—once you get the hang of the process, you’ll be solving these problems like a champ. Let’s break it down and make it easy.
What’s a Word Problem Anyway?
A word problem is just a math question wrapped up in a little story. Instead of handing you a simple equation to solve, the GRE gives you a situation. Your job is to figure out what numbers and relationships are involved and then do the math to get the answer.
Example:
"A car is going 60 miles per hour. If it’s already traveled 120 miles, how long will it take to reach 300 miles?"
Word problems are all about testing your ability to:
- Turn words into math equations
- Understand how the numbers relate to each other
- Apply some basic math skills to get to the right answer
Main Features of GRE Word Problems
GRE word problems come in different shapes and sizes, but they all have a few things in common. Here’s what you’ll typically see:
- Real-Life Scenarios
Expect stuff like travel, ages, work, rates, and percentages. Basically, the GRE throws everyday situations at you, but with a math twist. - Multiple Steps
This isn’t just basic math. GRE word problems usually require a few steps to solve. You’ll probably need to work through one part of the problem before moving to the next. - Tricky Language
Be on the lookout for words like “more than,” “less than,” “at least,” or “no more than.” These words can change how you need to set up your equation, so pay attention.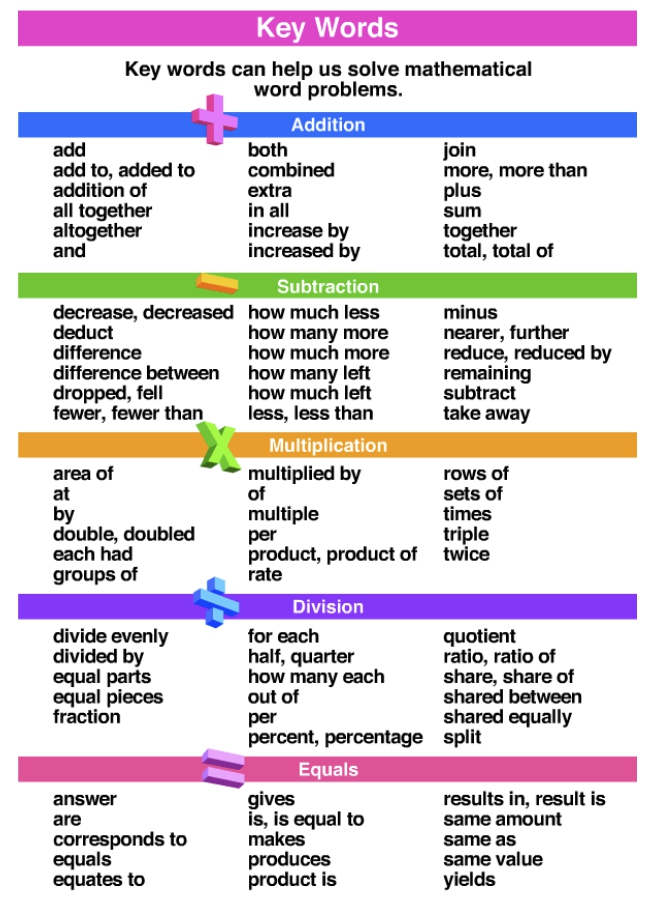
- Data Overload or Gaps
Some problems will give you extra info to mess with your head, while others will leave out key details that you’ll need to figure out.
Criteria of Word Problems
Here’s the trick to conquering these bad boys: understand what’s being asked, simplify the problem, and practice a lot. Let’s dive in.
1. Distance, Rate, and Time Problems
These problems revolve around the relationship:
Distance=Rate×Time

You might be asked to calculate one variable when the other two are given or solve multi-part scenarios involving two objects moving in different directions.
Key Indicators:
- Words like “speed,” “time,” “travel,” or “meet.”
- Involves vehicles, trains, or people moving at different speeds.
- Can involve upstream/downstream or round-trip scenarios.
Common Variations:
- Objects traveling toward or away from each other.
- Relative speeds (e.g., one object overtaking another).
- Multi-leg journeys with different speeds or times.
Example:
2. Work Problems
Work problems focus on how much of a task is completed in a given time. The formula is:
Work Done=Rate×Time
Key Indicators:
- Involves individuals or machines completing tasks.
- Often mentions “working together” or “alone.”
- Time is the most common unknown variable.
Common Variations:
- Two workers completing a task together vs. individually.
- Tasks with different rates (e.g., one worker is faster).
- Tasks are split into multiple phases.
Example:
3. Balancing or Mixture Problems
These involve mixing items with different properties (e.g., price, concentration). The goal is to balance or find averages.
Key Indicators:
- Words like “mix,” “combine,” or “solution.”
- Involves ratios, averages, or weighted values.
- Requires balancing quantities or properties.
Common Variations:
- Mixing two solutions to achieve the desired concentration.
- Combining items of different costs to find the total price.
- Splitting mixtures into parts.
Example:
4. Item or Unit Problems
These problems deal with quantities, unit prices, and costs.
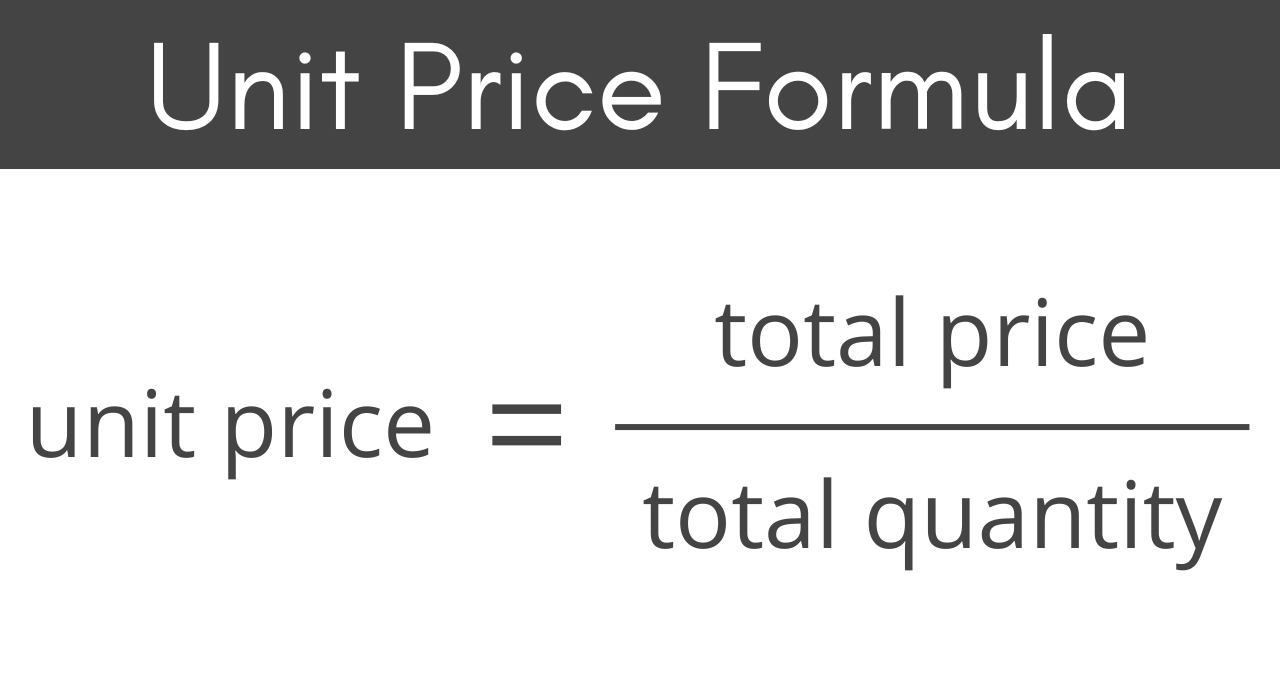
Key Indicators:
- Includes prices, discounts, or total costs.
- Focuses on “per unit” rates (e.g., price per pen).
- Often involves finding combinations of items.
Common Variations:
- Budget constraints with multiple items.
- Discounts or sales prices.
- Finding the total number of items bought.
Example:
5. Age Problems
These revolve around relationships between people’s ages at different times.

Key Indicators:
- Includes phrases like “years ago” or “in the future.”
- Involves age differences or ratios.
Common Variations:
- Comparing current ages with past or future ages.
- Solving for multiple unknowns using age relationships.
Example:
6. Money Problems (Profit and Loss)
These problems deal with cost price (CP), selling price (SP), and profit or loss percentages.
Key Indicators:
- Mentions profit, loss, discounts, or interest.
- Involves finding percentages or missing values.
Common Variations:
- Calculating profit or loss percentage.
- Determining selling price for desired profit.
- Investment problems with simple/compound interest.
Example:
7. Percentage Problems
These involve finding parts, increases, or decreases relative to a whole.

Key Indicators:
- Words like “percentage,” “increase,” or “decrease.”
- Often involves comparisons or changes over time.
Common Variations:
- Percentage change (increase or decrease).
- Part-whole relationships.
- Discounts and final prices.
Example:
8. Proportion Problems

These involve maintaining consistent ratios or scaling.
Key Indicators:
- Words like “proportion,” “ratio,” or “scale.”
- Involves quantities that grow or shrink proportionally.
Common Variations:
- Scaling recipes or mixtures.
- Calculating unknown quantities using ratios.
Example:
9. Probability and Counting Problems
These focus on the likelihood of events or arrangements.
Key Indicators:
- Words like “probability,” “chance,” or “arrangements.”
- Often requires finding total outcomes or combinations.
Common Variations:
- Basic probability (e.g., dice, coins).
- Combinations and permutations.
Example:
Word Problem Examples
Example 1:

Solution:
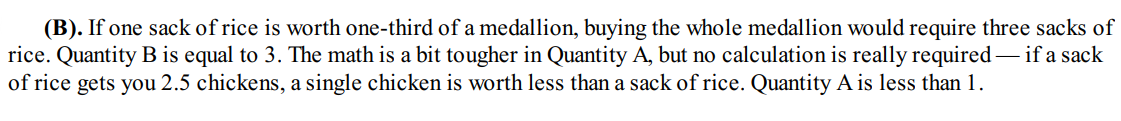
Example 2:

Solution:
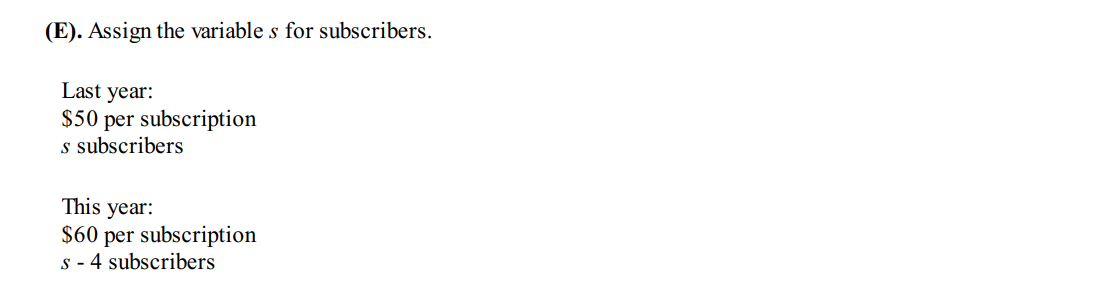
Example 3:
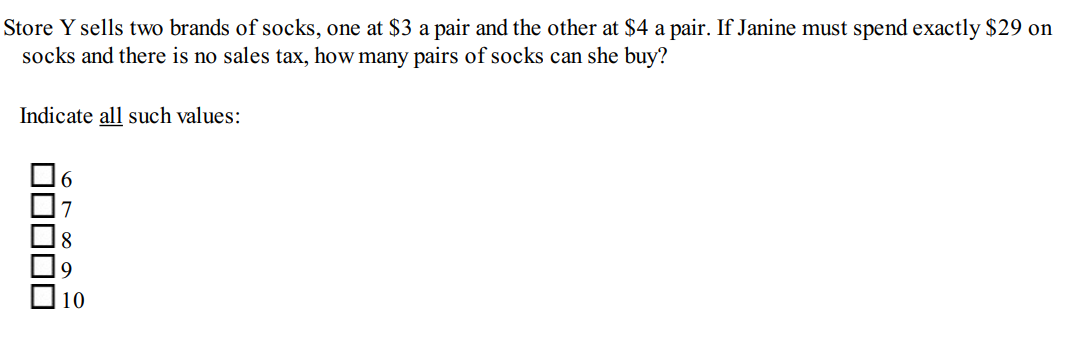
Solution:

Example 4:
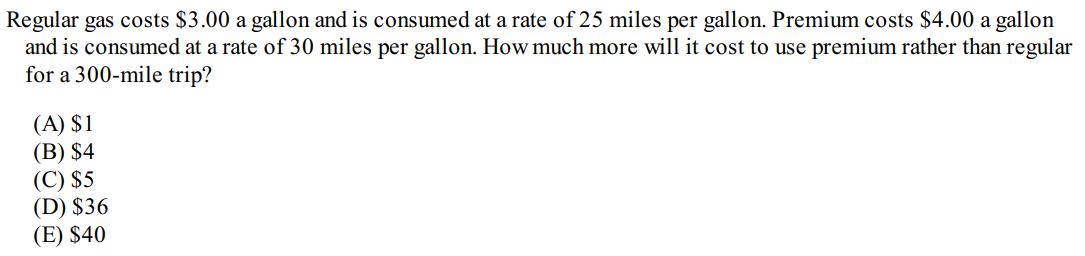
Solution:

Example 5:
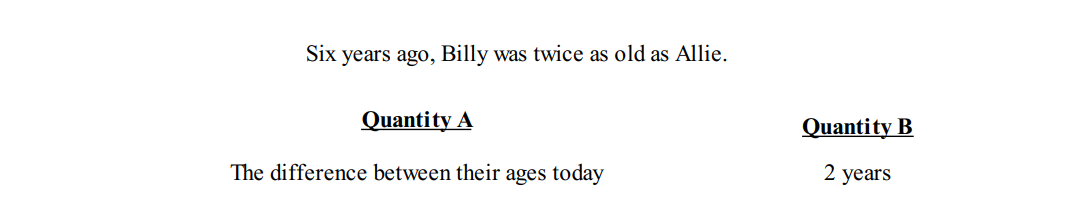
Solution:

Example 6:

Solution:

Example 7:
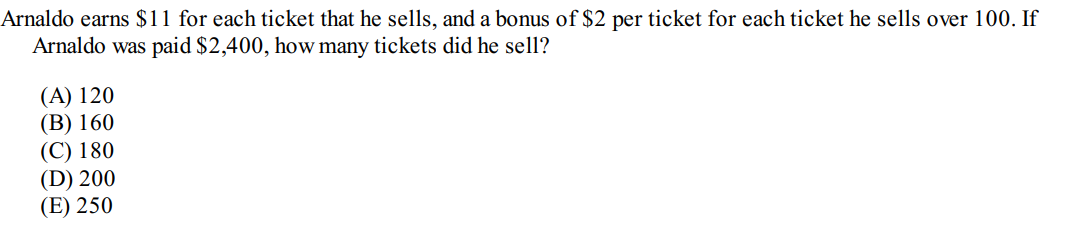
Solution:

Example 8:

Solution:

Example 9:

Solution:

Example 10:
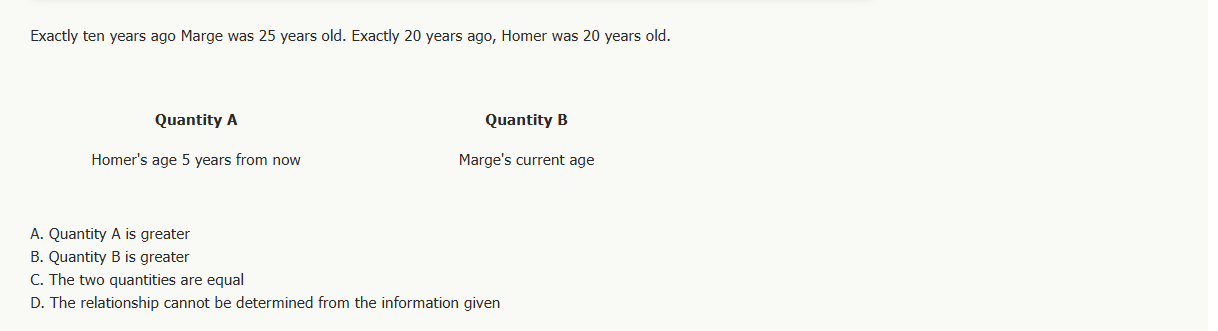
Solution:

What is a Two-Variable Word Problem?
A two-variable word problem involves two unknowns—basically, two things you need to solve for. The problem will give you some kind of relationship between the two variables, and your goal is to use that info to figure out their values.
Example: "The sum of two numbers is 20. One number is 4 less than twice the other. What are the two numbers?"
In this case, you’re dealing with two unknowns (the two numbers), and you need to use the given relationships to solve for both.
How to Solve Two-Variable Word Problems
Solving these types of problems usually comes down to setting up two equations with two unknowns and solving them together. This method is known as solving a system of equations. Here's a quick breakdown of how to tackle them:
1. Translate the Words into Equations
- Identify the two unknowns (the things you need to find).
- Write an equation for each relationship between the variables.
2. Set Up the System of Equations
- Often, you’ll get two relationships that involve both variables. You’ll need to combine those into a system of equations.
3. Solve the System of Equations
- You can solve the system in one of three ways: substitution, elimination, or graphing. The first two methods are the most commonly used for GRE word problems.
Common Techniques for Solving Two-Variable Problems
1. Substitution Method
This method is great when one of the equations is easy to solve for one variable.
Steps:
- Solve one of the equations for one variable (e.g., x or y).
- Substitute that expression into the other equation.
- Solve for the remaining variable.
- Substitute that solution back into one of the original equations to find the second variable.
2. Elimination Method
The elimination method is useful when you can add or subtract the equations to eliminate one of the variables.
Steps:
- Multiply one or both of the equations to make the coefficients of one of the variables the same (or opposites).
- Add or subtract the equations to eliminate that variable.
- Solve for the remaining variable.
- Substitute that solution back into one of the original equations to find the second variable.
Let’s Work Through an Example
Solution:
2 Variable Word Problem Examples:
Example 1:

Solution:

Example 2:

Solution:

Example 3:

Solution:

