Let's know about inequalities and absolute values as a part of your GRE journey, and definitely it's gonna be a good learning segment for you.
Inequalities
An inequality is a mathematical statement that compares two expressions, indicating that one is larger, smaller, or equal to the other within certain bounds. Unlike equations, inequalities often have multiple solutions, represented as ranges or sets of values.
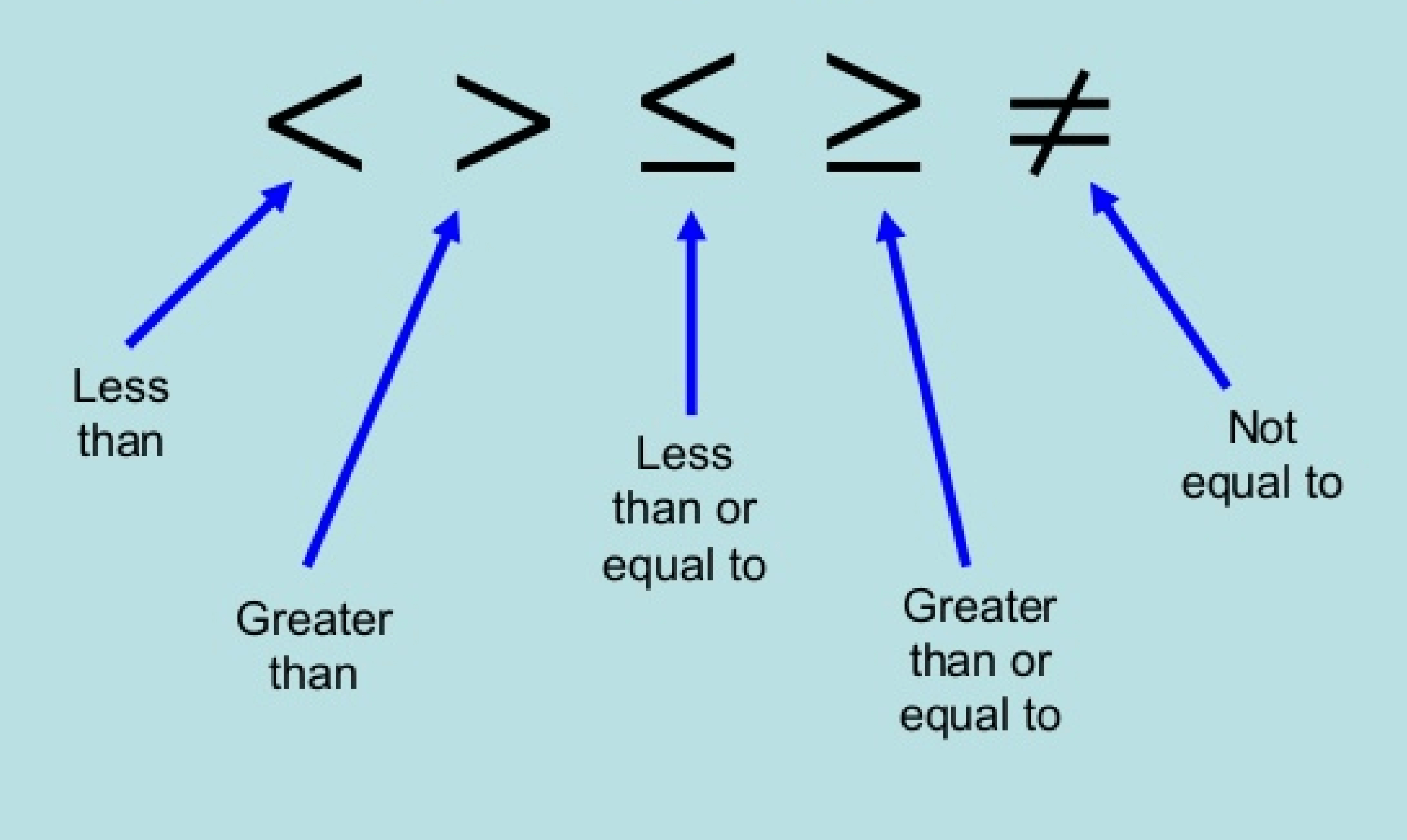
Types of Inequalities
1. Greater Than Inequality ( > )
This inequality indicates that a value is strictly larger than another.
Example: x > 3
- x can take all real values greater than 3.
2. Less Than Inequality ( < )
This indicates that a value is strictly smaller than another.
Example: y < 2
- y can take all real values less than 2.
3. Greater Than or Equal To Inequality ( ≥ )
This inequality includes the value itself along with all larger values.
Example: x ≥ 5
- x can take all real values greater than or equal to 5.
4. Less Than or Equal To Inequality ( ≤ )
This includes the value itself along with all smaller values.
Example: y ≤ 3
- y can take all real values less than or equal to 3.
5. In-Between Inequality
This inequality represents a range of values between two bounds.
Example: -2 ≤ x < 5
- x can take all values greater than or equal to −2-2−2 and less than 5.
Rules and Properties of Inequalities
- Addition and Subtraction:
Adding or subtracting the same value on both sides of an inequality preserves the inequality.- If a > b , then a+c > b+c
- Similarly, a−c > b−c
- Multiplication and Division:
- By a Positive Number: The inequality remains unchanged.
- If a > b, then ka > kb for k > 0
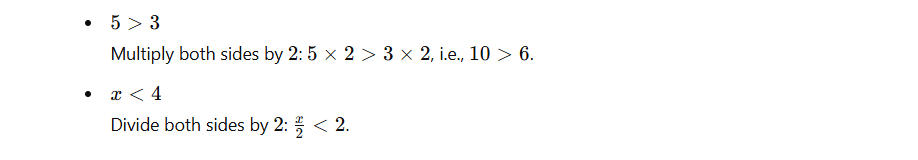
- If a > b, then ka > kb for k > 0
- By a Negative Number: The direction of the inequality reverses.
- If a > b, then ka < kb for k < 0
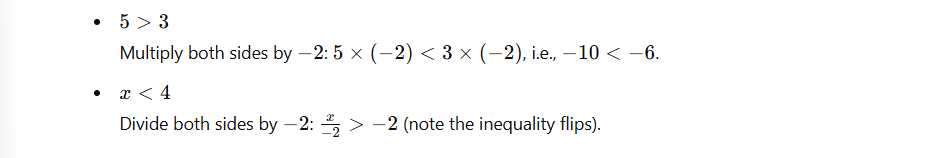
- If a > b, then ka < kb for k < 0
- By a Positive Number: The inequality remains unchanged.
- Transitive Property:
- If a > b and b > c, then a > c.
- Combining Inequalities:
- Inequalities with overlapping ranges can be combined.
- Example: If x > 3 and x < 7, then 3 < x < 7
- Reciprocal Property:
Taking the reciprocal of both sides reverses the inequality if the numbers are positive.- If a > b > 0, then 1/a < 1/b.
6. Squaring Inequalities
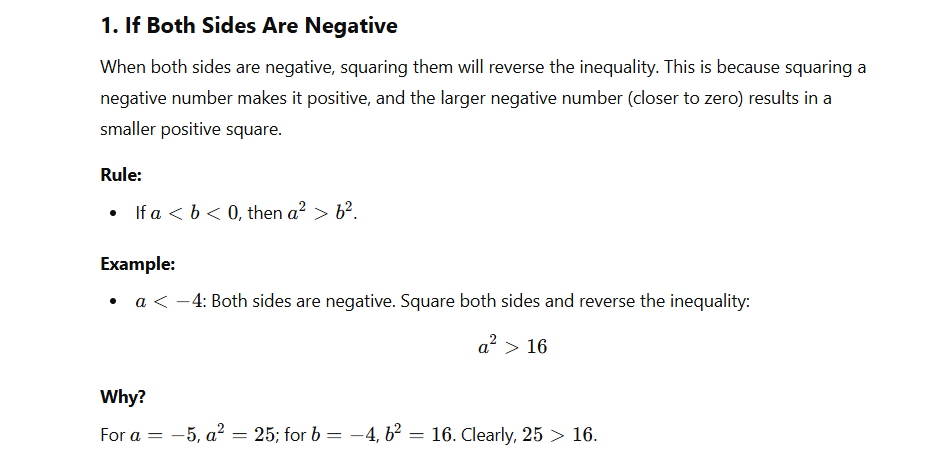


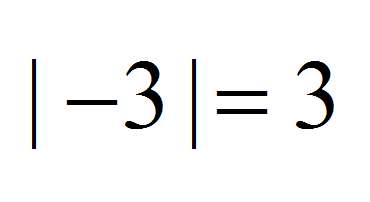
Absolute Values
The absolute value of a number measures its distance from 0 on the number line, disregarding its sign. Represented as ∣x∣|x|∣x∣, the absolute value function outputs only non-negative results.
Key Properties of Absolute Value
Absolute Value Inequalities
Inequalities involving absolute values can be categorized into two main types, each requiring specific strategies to solve:
Case 1: ∣x∣ < c (Less Than)
When ∣x∣<c, it implies that x is within c units of 0:
−c<x<c
Example: Solve ∣x∣<4.
- Rewrite as: −4<x<4
- Solution: x lies between −4 and 4.
Case 2: ∣x∣ > c (Greater Than)
When ∣x∣ > c , it implies that x lies outside the range of −c to c:
x < −c or x > c
Example: Solve ∣x∣ > 3
- Rewrite as: x < −3 or x >3
Graphical Representation of Absolute Value Inequalities
Absolute value inequalities can be visualized on a number line to better understand their solutions:
- For ∣x∣<4 , shade the region between −4 and 4.
- For ∣x∣≤4 , shade the region between −4 and 4 .
- For ∣x∣ > 3, shade the regions outside −3 and 3.
Graphing is particularly useful in GRE quantitative comparison questions where multiple ranges overlap.
GRE Examples
Question 1
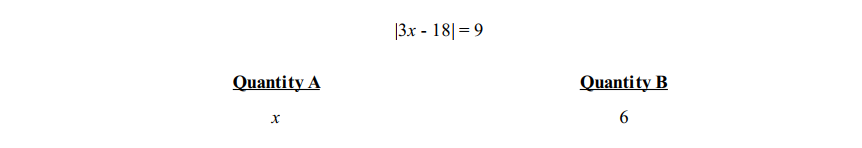
Solution:

Question 2

Solution:

Question 3
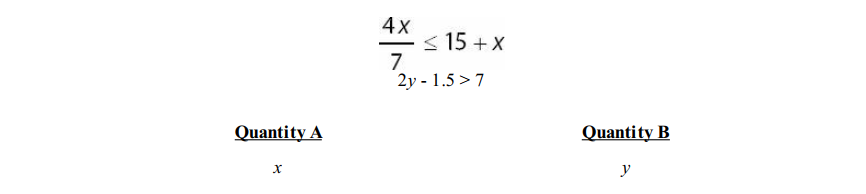
Solution:

Question 4
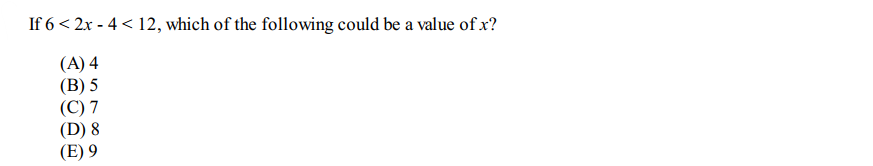
Solution:

Question 5
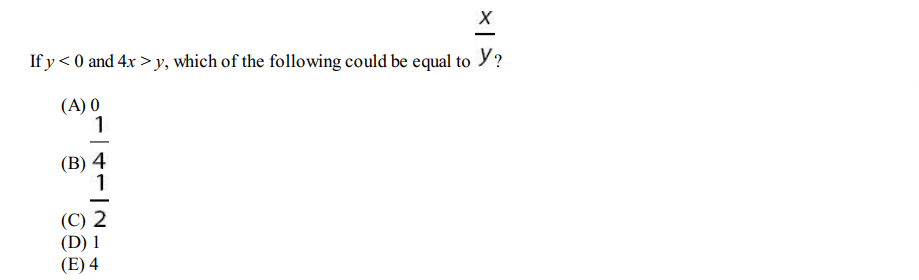
Solution:

Question 6
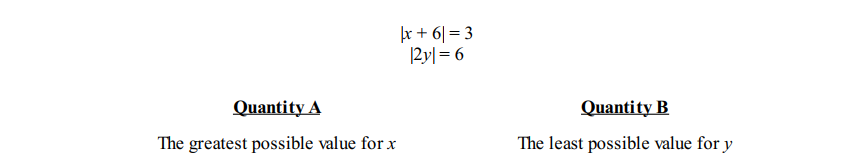
Solution:

Question 7

Solution:
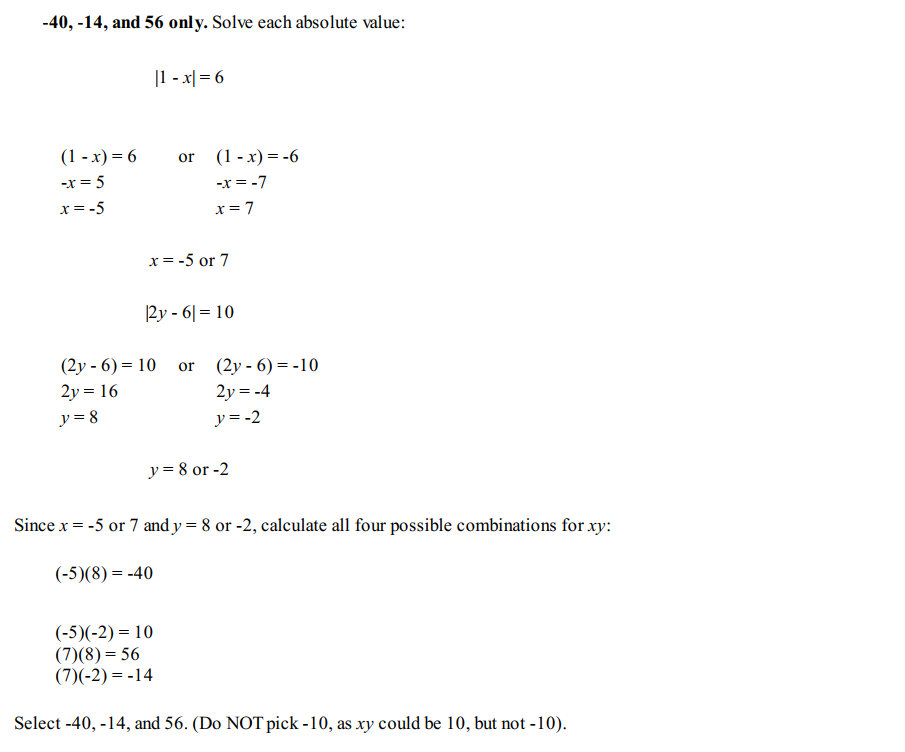
Question 8

Solution:
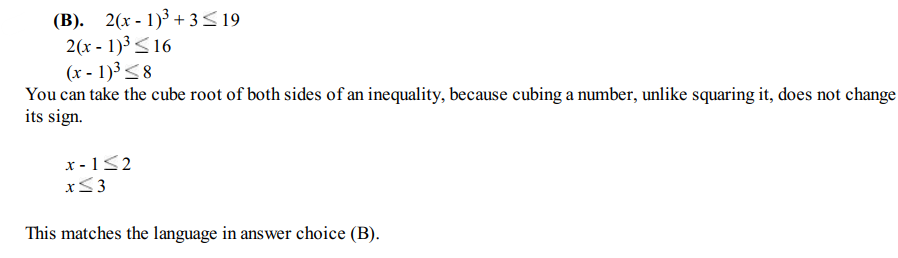
Question 9

Solution:

Question 10

Solution:
Question 11

Solution:

Question 12
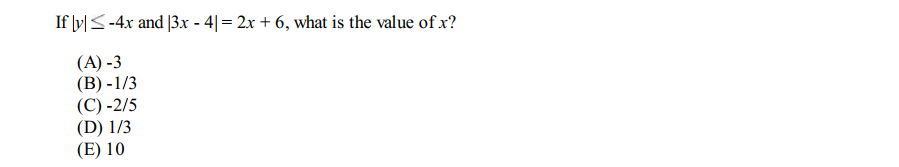
Solution: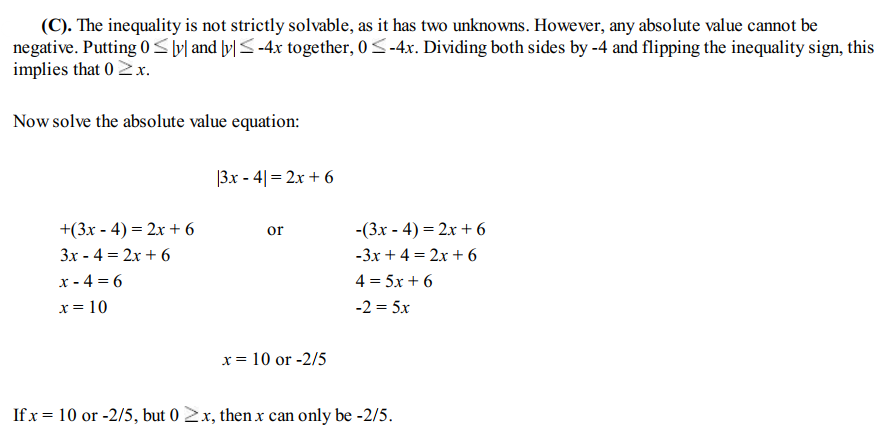
Question 13

Solution:

Question 14
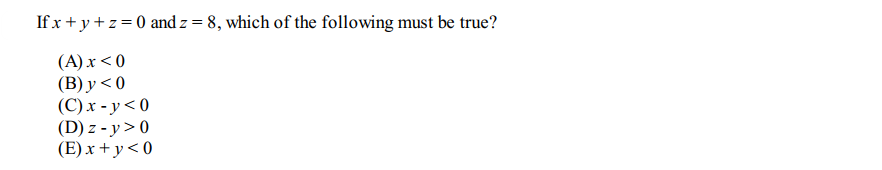
Solution:

Question 15
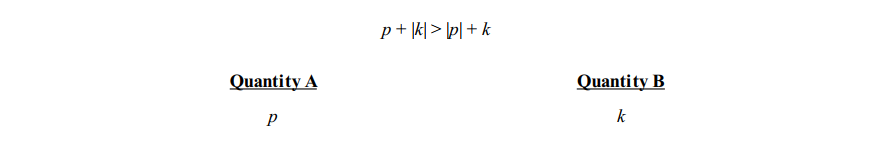
Solution:

Question 16
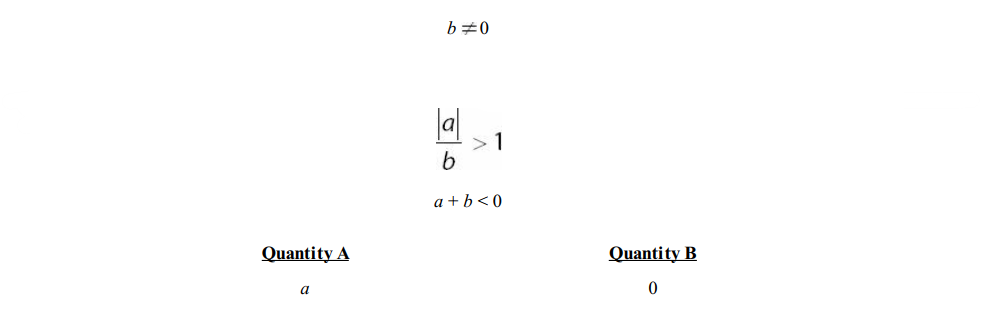
Solution:

Question 17
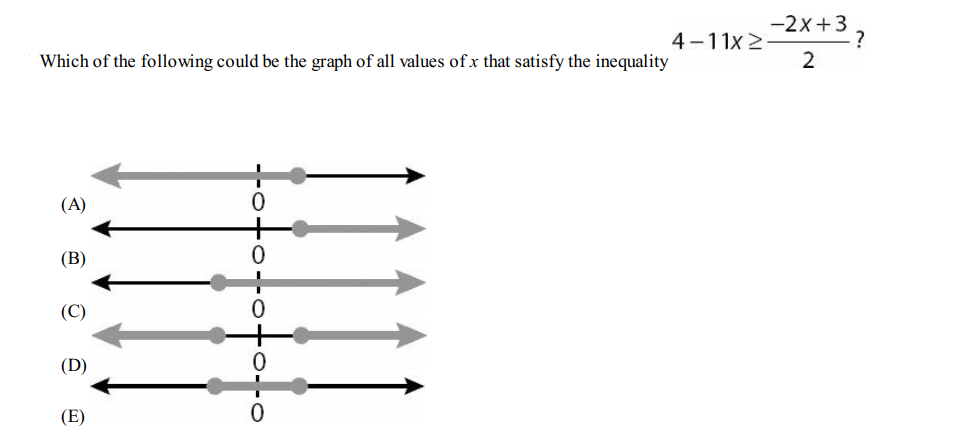
Solution:

Question 18
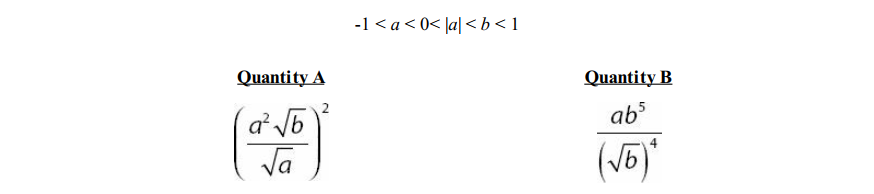
Solution:


Question 19
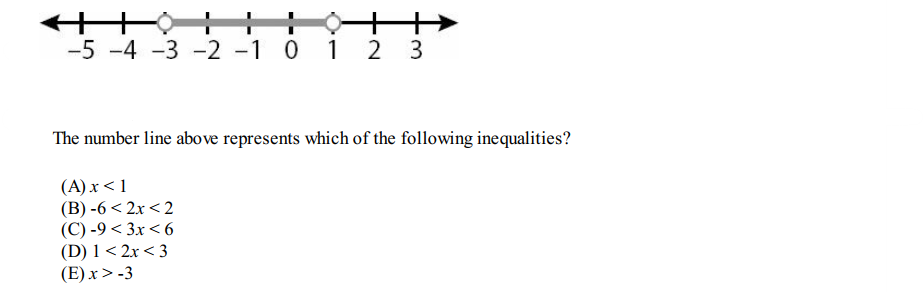
Solution:

Question 20

Solution:

Question 21
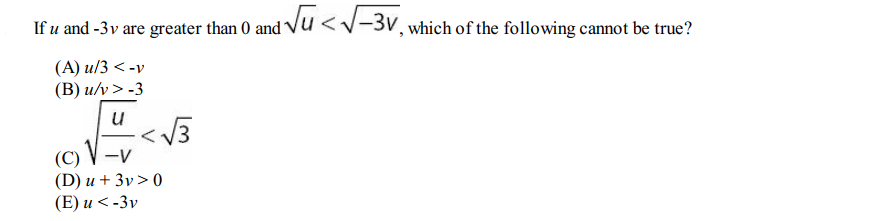
Solution:

