This article will cover the basis of Fractions, Decimals, and Percent which are very important topics for Quant GRE. After the theory part related examples are given:
What is a Fraction?
A fraction represents a part of a whole and is written as a/b, where:
- a (numerator) indicates how many parts we have.
- b (denominator) indicates the total number of equal parts the whole is divided into.
For example:
- 1/2 means one part out of two equal parts.
- 3/4 means three parts out of four equal parts.
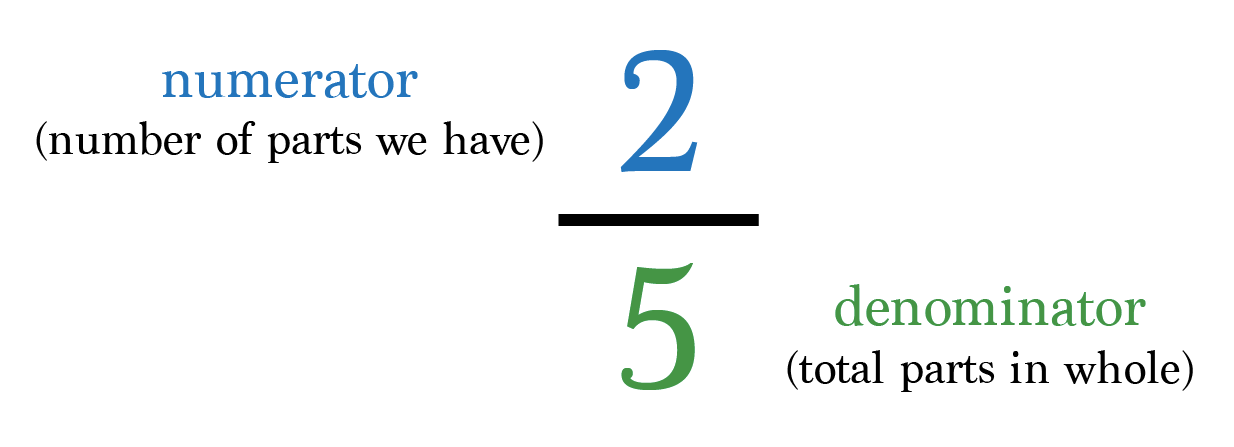
Equivalent Fractions
Equivalent fractions are fractions that represent the same value, even though their numerators and denominators may be different. To create equivalent fractions, you multiply or divide the numerator and denominator by the same non-zero number.
Creating Equivalent Fractions (Multiplication):
To generate an equivalent fraction, multiply both the numerator and denominator by the same number.
- Example: 2/3 * 2/2 = 4/6
Here, 2/3 and 4/6 are equivalent.
Creating Equivalent Fractions (Division):
Divide the numerator and denominator by their greatest common divisor (GCD) to simplify.
- Example: 8/12 / 4/4 = 2/3
Here, 8/12 simplifies to 2/3.
Simplifying Fractions
To simplify a fraction, divide the numerator and denominator by their greatest common divisor (GCD), reducing it to its simplest form.
- Example: 9/12
The GCD of 9 and 12 is 3.
Simplified: 9÷3 / 12÷3 = 3/4
Types of Fractions
Fractions are classified into three types based on the relationship between the numerator and denominator:
1. Proper Fractions
A fraction where the numerator is smaller than the denominator.
- Example: 2/5 , 3/7
2. Improper Fractions
A fraction where the numerator is greater than or equal to the denominator.
- Example: 7/8 , 9/8
3. Mixed Fractions
A combination of a whole number and a proper fraction.
- Example: 2 ⅓ , which is equivalent to 7/3.
To convert a mixed fraction into an improper fraction:
- Multiply the whole number by the denominator.
- Add the numerator to the result.
- Write the sum as the new numerator over the denominator.
Example:
Fractions on a Number Line
Fractions can be represented on a number line by dividing the space between 0 and 1 (or other integers) into equal parts.
- Example: To plot 3/4, divide the segment between 0 and 1 into 4 equal parts. 3/4 will be at the third mark.
For improper fractions like 7/4, plot it beyond 1. Divide the space between 1 and 2 into 4 equal parts, and 7/4 will fall on the third mark past 1.
Adding and Subtracting Fractions
1. Fractions with the Same Denominator
Simply add or subtract the numerators and keep the denominator unchanged.
- Example: 2/5+3/5=5/5
2. Fractions with Different Denominators
- Find the least common denominator (LCD) of the fractions.
- Rewrite each fraction with the LCD as the denominator.
- Add or subtract the numerators.
Example: 1/3+1/4=4/12+3/12= 7/12
Multiplying Fractions
To multiply two fractions:
- Multiply the numerators.
- Multiply the denominators.
- Simplify the result if needed.
Example: 2/3 × 4/5 = (2×4)/(3×5) = 8/15
Dividing Fractions
To divide fractions:
- Flip the second fraction (find its reciprocal).
- Multiply the first fraction by the reciprocal of the second.
- Simplify if necessary.
Example: (3/4) / (2/5) = 3/4 * 5/2 = 15/8
Comparing Fractions
To compare fractions:
- With the same denominator: Compare the numerators directly.
Example: 3/8 < 5/8, since 3 < 5. - With different denominators: Find a common denominator, then compare numerators.
Example: 2/3 vs. 3/5
Convert: 2/3 = 10/15. 3/5 = 9/15
Since 10 > 9, 2/3> 3/5. - Cross-Multiplication Method: Multiply the numerator of each fraction by the denominator of the other and compare.
Example: Compare 3/4 and 2/3:
3×3=9, 2×4=8 Since 9 > 8, 3/4>2/3
What is a Decimal?
A decimal is a way to represent numbers that are not whole. It uses a decimal point to separate the whole number part from the fractional part. For example:
- 12.512.512.5: The number 12 is the whole part, and 0.5 represents the fractional part.
Decimals are based on the base-10 system, where each place value is 10 times the value of the place to its right.
Place Value and Face Value in Decimals
Place Value:
The place value of a digit in a decimal depends on its position relative to the decimal point. Each position represents a power of 10.
- Positions to the left of the decimal point:
- Hundreds, tens, ones (e.g., 345.67 → 3 is in the hundreds place).
- Positions to the right of the decimal point:
- Tenths, hundredths, thousandths, etc. (e.g., 0.456 → 4 is in the tenths place).
Position | Value (Example: 456.789) |
Hundreds | 4 |
Tens | 5 |
Ones | 6 |
Tenths | 7 |
Hundredths | 8 |
Thousandths | 9 |
Face Value:
The face value of a digit is the digit itself, regardless of its position in the number.
- Example: In 456.789456.789456.789:
- The face value of 5 is 5.
- The face value of 8 is 8.
Rounding Decimals
Rounding decimals is the process of reducing the number of digits after the decimal point while keeping the value as close as possible to the original number. Rounding is commonly used to simplify numbers for practical use.
Steps to Round a Decimal:
- Identify the place to round to (e.g., nearest tenth, hundredth).
- Look at the digit to the right of the rounding place:
- If it’s 5 or greater, round up (add 1 to the rounding place).
- If it’s less than 5, round down (leave the rounding place as is).
- Truncate all digits after the rounding place.
Examples:
- Round 12.346 to the nearest tenth:
- Look at the hundredths place (4). Since it’s less than 5, 12.346 rounds to 12.3.
- Round 0.7890.7890.789 to the nearest hundredth:
- Look at the thousandth place (9). Since it’s greater than 5, 0.789 rounds to 0.79.
Comparing Decimals
To compare decimals:
- Start from the leftmost digit and compare each place value.
- Add trailing zeros if necessary to make the decimals have the same number of digits.
Examples:
- Compare 0.45 and 0.450: Both are equal because trailing zeros don’t change the value.
- Compare 0.8 and 0.75: Since 0.8>0.75,0.8 is larger.
Operations with Decimals
1. Addition and Subtraction
Align the decimal points and perform the operation as you would with whole numbers. Add trailing zeros if necessary to match the number of digits.
- Example: 12.5+0.75=13.2512.5 + 0.75 = 13.2512.5+0.75=13.25
2. Multiplication
Multiply as whole numbers, ignoring the decimal points. Then, place the decimal in the product based on the total number of decimal places in the factors.
- Example: 1.2×0.3=0.36(1 decimal place in 1.2 + 1 decimal place in 0.30).
3. Division
Move the decimal point in the divisor to make it a whole number, then adjust the dividend accordingly. Divide as usual and place the decimal in the quotient.
- Example: 12.6÷0.2=63 (move the decimal in 0.20 one place to the right, and do the same for 12.6).
Converting Between Decimals and Fractions
1. Decimal to Fraction:
- Write the decimal as a fraction with a denominator of 10,100,1000 etc., based on the number of decimal places.
- Simplify the fraction.
- Example: 0.25=25/100=1/4
2. Fraction to Decimal:
- Divide the numerator by the denominator.
- Example: 1/4=1÷4=0.25.
Decimals in Real Life
Decimals are used extensively in:
- Money: $12.50(twelve dollars and fifty cents).
- Measurements: 5.75 inches (five and three-quarters of an inch).
- Scientific Data: 0.001 represents small quantities in physics or chemistry
What is a Percent?
A percent is a fraction of 100. It represents a part of a whole, where the whole is divided into 100 equal parts. The symbol % denotes percent.
- Example: 50% means 50 out of 100, or 50/100=0.5.
Key Formulas:
- To convert a percentage to a fraction: x%=x/100.
- To convert a percentage to a decimal: x%=x÷100.
- To calculate a percentage of a number: Percentage Value=(Percent×Number)÷100=(Percent×Number)÷100
- Example: What is 20% of 150?
Value=(20×150)/100=30
1. Simple Interest
Simple interest is the interest calculated on the original principal over a period of time.
Formula:
Simple Interest (SI)=(Principal (P)×Rate (R)×Time (T))/100
- Example: A principal of $1000 is invested at a rate of 5% for 3 years.
SI=1000×5×3/100=150
Total amount = Principal + Interest = $1000 + $150 = $1150.
2. Compound Interest
Compound interest is calculated on the principal and the accumulated interest from previous periods.
Formula:
Compound Interest (CI)=Principal×(1+Rate/100)^Time−Principal
Steps to Calculate CI:
- Add the rate as a fraction to 1 (1+R/100).
- Raise this value to the power of the time (T).
- Multiply by the principal and subtract the original principal.
3. Percentile
A percentile represents a value below which a certain percentage of data falls. It is commonly used in exams, surveys, and data analysis.
Formula:
Percentile Rank=Number of values below the scoreTotal number of values×100\text{Percentile Rank} = \frac{\text{Number of values below the score}}{\text{Total number of values}} \times 100 Percentile Rank=Total number of valuesNumber of values below the score×100
- Example: In a test of 100 students, if your score ranks 80th, your percentile is:
Percentile= 80/100×100 =80%
This means you scored higher than 80% of the class.
4. Consecutive Percentage Change
When a percentage change is applied multiple times, the overall change is not additive but multiplicative.
5. Undoing a Percent Change
To reverse a percentage change and find the original value, divide the final value by the percentage multiplier.
6. Population Formula
Population growth or decay often uses percentages to calculate changes over time.
Conversions
1. Converting Fractions to Decimals
Divide the numerator by the denominator.
Example: 3/4=3÷4=0.75
Repeating decimals: For fractions like 1/3, you get 0.333... You can write this as 0.33, overline .3, depending on the question.
Tip for the GRE: Memorize common fractions and their decimal equivalents to save time.
| Fraction | Decimal |
|---|---|
| 1/2 | 0.5 |
| 1/3 | 0.333... |
| 1/4 | 0.25 |
| 1/5 | 0.2 |
| 2/3 | 0.666... |
| 3/4 | 0.75 |
2. Converting Decimals to Fractions
Write the decimal as a fraction and simplify.
Example: 0.75=75/100 = 3/4.
For repeating decimals, use the formula for conversion:
- Let x=0.666...
- Multiply x by 10 (or a power of 10, depending on the number of repeating digits): 10x==6.666...
- Subtract: 10x−x=9x
3. Converting Fractions to Percentages
- Multiply the fraction by 100 and add the percent sign.
Example: 3/4=0.75×100=75%
4. Converting Decimals to Percentages
- Multiply the decimal by 100 and add the percent sign.
Example: 0.25×100=25%.
5. Converting Percentages to Fractions
- Write the percentage as a fraction over 100 and simplify.
Example: 25%=25/100 = 1/4.
6. Converting Percentages to Decimals
- Divide the percentage by 100.
Example: 75%=75÷100=0.75.
Memorize Common Equivalents
| Fraction | Decimal | Percentage |
|---|---|---|
| 1/2 | 0.5 | 50% |
| 1/3 | 0.333... | 33.33% |
| 2/3 | 0.666... | 66.67% |
| 1/4 | 0.25 | 25% |
| 3/4 | 0.75 | 75% |
| 1/5 | 0.2 | 20% |
| 1/8 | 0.125 | 12.5% |
Fractions Questions
1. Quantitative Comparison Question

Solution:

2. Multiple-choice Questions — Select One Answer Choice

Solution:

3. Multiple-choice Questions — Select One or More Answer Choices

Solution:

4. Numeric Entry Question

Solution:

Decimal Questions
1. Quantitative Comparison Question

Solution:

2. Multiple-choice Questions — Select One Answer Choice

Solution:

3. Multiple-choice Questions — Select One or More Answer Choices

Solution:

4. Numeric Entry Question

Solution:
Percentage Questions
1. Quantitative Comparison Question

Solution:

2. Multiple-choice Questions — Select One Answer Choice

Solution:

3. Multiple-choice Questions — Select One or More Answer Choices

Solution:
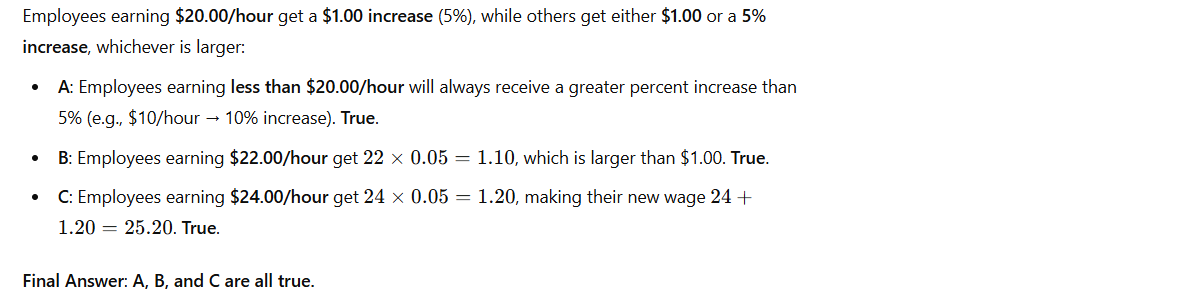
4. Numeric Entry Question

Solution:

